%20(1)-1.png?width=1080&name=Title_%20How%20to%20Study%20Efficiently%20for%20Hours%20On%20End%20(With%20the%20Help%20of%20a%20Tomato)%20(1)-1.png) If you are reading this, I can tell you’ve mastered solving simple linear equations. You’ve mastered the art of balance. You know that whatever you do to one side of the equal sign, you must do to the other. You can perform inverse operations until the cows come home, and you are a pro at isolating the variable. I bet you even check your work by plugging your answer back into the original equation, math whiz kid that you are. You could solve the following problem without breaking a sweat.
If you are reading this, I can tell you’ve mastered solving simple linear equations. You’ve mastered the art of balance. You know that whatever you do to one side of the equal sign, you must do to the other. You can perform inverse operations until the cows come home, and you are a pro at isolating the variable. I bet you even check your work by plugging your answer back into the original equation, math whiz kid that you are. You could solve the following problem without breaking a sweat.
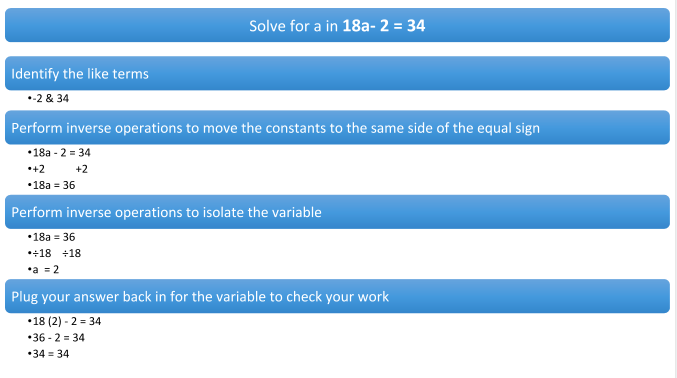
Now it’s time to crank things up a notch. Take a look at the following equation. What do you notice is different about it than equations we have worked with before?
8y - 14 = 2y + 22
You probably recognized that in this problem there are TWO terms that contain our variable, 8y and 2y. Moreover, they are on different sides of the variable. Although this may look daunting, we only have to add one more step to our trustworthy process, and we will be solving equations with variables on both sides of the equal sign in no time.
A reminder about like terms: like terms are mathematical terms that have the same variable and same exponent, but they do not need to have the same coefficient or same sign. For example, 2y2 and -14y2 are like terms because they both are attached to a y-variable raised to the second power. The fact that they have different coefficients and that one is positive while the other is negative is inconsequential. By contrast, 3y3 and 3y are not like terms because the variables have different exponents. When solving equations with variables on both sides of the equation, it is critical that you can correctly identify like terms, so you know what terms can be combined.
With that reminder under our belt, let’s jump into solving some problems!
Step 1: Figure out what you are solving for.
This step is perhaps the easiest. Think about the equation 8y - 14 = 2y + 22. We know that the equal sign signifies that when we plug in a certain number for y, both sides will result in the same number. If we envision the problem as a scale, we want to know what y needs to be for the two sides to be perfectly balanced.

Therefore, our task is to figure out what value of y would make this equation true.
Step 2: Identify like terms.
Just like solving equations with only one term containing a variable, it is important to first identify the like terms in our problem. This will help us know what terms to move in order to make it easier to manipulate the equation. Color-coding the variable-terms and the constants can be a great tool here. I will make the variable-terms red and the constants blue.
Example 1: 8y - 14 = 2y + 22
Example 2: -2y + 8 = -1.5y - 30
Step 2: Move the smaller variables-term first.
I’m going to let you in on a secret. It doesn’t matter if you move the variable-terms or the constants first. However, I find that it is usually easier to move the variable first so that the equation looks like a simple linear equation. I always begin by moving the term with the lower coefficient. In order to do this, perform the inverse operation, (i.e. if you have 2y on one side, subtract 2y from each side.) Take a look the examples below:
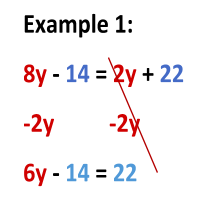

As you can see, when you cancel out the variable one side, we are left with a simple linear equation. From here, we can use the exact same process we have already mastered in order to solve for y!
Step 3: Combine the constants.
From here we use inverse operations to move the constants to the opposite side of the equal sign from the variable. HOT TIP: the inverse operation is how you “undo” an operation. It does not matter which side the variable ends up on, as long as the constants are on the other side.


Step 4: Isolate the variable.
These final equations probably look familiar to you. You know that in order to get to our final answer, we need to get the variable alone by “undoing” the operation. For both of these final equations, we are going to “undo” by dividing by the coefficient in front of the variable.
Here’s a hack for when you are working with fractional coefficients, as in Example 2. Remember that dividing by a fraction is the same as multiplying by its inverse. For example, instead of dividing by ½ or 0.5, you could simply multiply by its inverse, 2 (the inverse of 1/2 is 2/1 because the numerator and denominator are switched.) The inverse trick is helpful if you can’t do it in your head and don’t have a calculator handy.
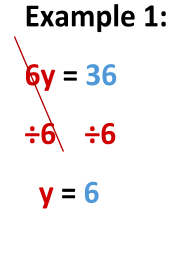
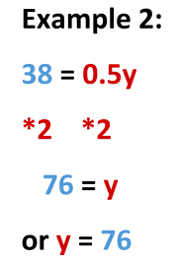
Step 5: Check your work.
It’s almost time for our victory lap, but not quite yet. Our final step is to plug in the answer we got for our variable, to see if it makes our equation true. It is very, very important that we use PEMDAS correctly when checking our work, otherwise a computational error could throw off all of that hard work. Let’s plug in our answers into our original equations to see how we did!


Now that you can solve equations with variables on both sides, a whole world of algebra problems will open up for you. Happy solving, and see you next time!
Mathematics – from elementary school math through high school math – is one of our most frequently requested subjects. Teaching math is notoriously difficult and we maintain a staff of mathematicians who are committed to the art of teaching. There is no course or standardized test that we do not have extensive experience teaching. We work with students who loathe math and students who love it, students who haven’t done math in a decade and students who work on mathematical problems every day.
Looking for middle school support? Check out our other blog posts below!
The Middle School Writers’ Workshop: 3 Steps to a Great Literary Essay Outline
5 Middle School Books for Reluctant Readers
How to solve linear algebraic equations

Comments