In the year 1202, Italian mathematician Leonardo Fibonacci published the extremely influential Liber Abaci (Book of Calculations). The book's most significant contribution was to bring to Europe the Hindu-Arabic number system that we all use today. But it also contained a curious thought experiment about the reproductive patterns of rabbits, which gave rise to one of the most famous sequences in math that would entertain and tantalize generations of mathematicians to come.

Do mathematicians dream of immortal rabbits?

The problem goes like this: Say that a rabbit comes of age when it is one year old. Having reached this mark of adulthood, each adult rabbit gives birth to one pair of rabbits, a male and a female, each month. Assume we start at time 0 with a single pair of rabbits. How many rabbits will there be at a given point in time?

To illustrate, we can begin by looking at the first few months. After one month passes, the baby rabbit pair grows to an adult. There is still 1 rabbit pair, who is now ready to have kids. In month two, our rabbit has a pair of twins, so the population grows to 2. We now have one adult pair and one baby pair. In month three, the adult gives birth again and last year's baby reaches adulthood. We now have 3 rabbits-- two adults and one baby. Next month, the two adults each have a baby so the population grows to 5 rabbits. And so on.

The sequence charting the rabbit population thus begins

1,1,2,3,5,...

We denote the nth element of the sequence by

Fibonacci's model of rabbit populations is not particularly sophisticated or accurate. For one thing, it imagines that a rabbit pair always reproduces exactly one male and one female. Much more glaringly, it conveniently ignores death. But by this point, you probably figured that the rabbits are only a pretext.

Mathematicians dream of immortal rabbits in order to study interesting math.

So what is interesting here? Let's take another look at the sequence:

1,1,2,3,5,8,13,21,...

You might notice a pattern: each term is precisely the sum of the previous two! How come? There's a simple reason. Each given year, the population consists of those rabbits who were around last year, plus the number of babies who are newly born:

This month's population = last month's population + number of newborns

But how do we count the newborn pairs? Well, newborns are precisely identified by their parents (since each rabbit has a unique parent pair in our simplified model). The eligible parents are exactly those who were in existence two months ago (since they must have had enough time to first become an adult and then give birth). So there we have it: the number of newborns exactly equals the population of two years ago. We can then update our equation:

This month's population = Last month's population + The population of two months ago

Or in a more concise form:

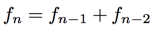
With the caveat that this formula only really makes sense if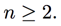 

This kind of formula is called a recurrence relation: it relates each term of the sequence to previous terms. It gives us a practical way of generating the sequence: each time simply add the previous two terms. We can now forget about rabbits, babies and adults, and simply follow an arithmetical rule. You can play with that to write the next few terms of the sequence.

Rate of growth

We now understand how the Fibonacci sequence behaves locally, that is, how each term relates to the ones that came immediately before it. But what if we wanted to understand the long-term behavior? One basic way to assess that is the rate of growth. How quickly does the rabbit population grow?

Here is one way to get a handle on the growth of the Fibonacci sequence. Start with the recurrence relation

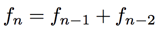
Now notice that 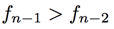 since the sequence is always increasing. Plugging in this inequality above,

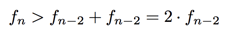
This is telling us that  more than doubles every two years. A quantity that doubles every fixed number of years is exponential. Thus, the Fibonacci sequence, though modest at first, in fact increases exponentially.

In search of an explicit equation

We have gained some insight into the long-term behavior of the Fibonacci sequence, but only in the form of a rough lower bound. In some sense we still lack a fully satisfactory understanding of the Fibonacci numbers. What if we wanted to get the 50th term of the sequence? We could compute it using the recurrence relation, but that would entail first calculating all the previous 49 terms before we get the answer. Is there a single explicit equation that describes the nth Fibonacci number without relying on the previous elements of the sequence?

There is certainly no immediately apparent answer. Fibonacci himself failed to come up with such an explicit formula in his book. The theory of linear difference equations deals with this type of question, but we will instead use the tool of generating functions, in order to showcase its power. But we must first take a short detour to the topic of power series.

Power Series

A power series is like a super-powered version of a polynomial. While a polynomial is a modest expression such as 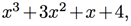 a power series has infinitely many terms. For example, consider the power series

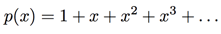
or

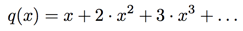
(where the ellipsis indicate that we keep going ad infinitum).

The first question that arises is, what does this even mean? How can you add together infinitely many terms? Indeed, if we tried to plug in x=1 into the above power series p(x), we get the infinite sum 1+1+1+..., which diverges to infinity. Even worse, if we try plugging in x=-1, we get the infinite sum 1-1+1-1+1-..., which I invite you to try to evaluate.

To avoid these tangles, we will be careful to refrain from thinking of power series as functions. We simply do not expect to be able to plug in a number and get out another number. Instead, a power series will be a formal expression, amounting simply to a choice of coefficient for each power 

At first, this might seem like a useless invention, merely dressing up a sequence of coefficients in the garb of a polynomial. The crucial point, however, is that even while power series cannot be viewed as functions, we can still perform algebra with them just as we do with polynomials: we can add, subtract, multiply (and sometimes even divide) power series with each other.

To illustrate the interesting algebra that can be done with power series, let's start with the simple power series

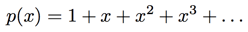
Consider what happens when we multiply by x:

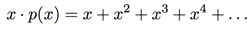
Observe that this is exactly the same as p(x), except missing a 1. That is,

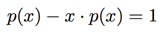
Factoring out , we get

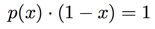
or

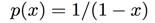
That is,

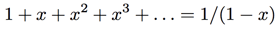
We have found a way to rewrite  from an infinite expression into a simple fraction!

Side note: I emphasized earlier that power series should not be thought of as functions. However, in the special case that -1<x<1, you can actually plug in x into the above equation and obtain a valid equation.

For example,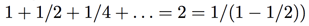 

We can also attempt to go in the other direction, converting a quotient of polynomials into a power series. For example, consider a fraction of the form We can relate this to our previous example by factoring out a -r from the denominator:

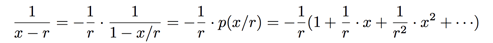
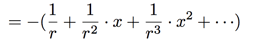
Challenge: If you want to practice your power series chops, try deriving an expression for the more complicated power series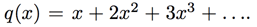

Hint: again, consider the difference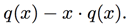

What does this equal?

I promised that power series will help us figure out an explicit equation for the Fibonacci numbers. This is where generating functions come in. 

Generating Functions

The idea of generating functions is simple. In order to understand sequences, we can transform them into power series by turning the elements of the sequence into power series coefficients. For example, if we start with the sequence 1,1,1,1,..., its generating function is the power series

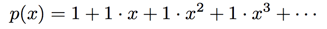
which we studied in the last section. If we start with the Fibonacci sequence 1,1,2,3,5,...,  its generating function is the power series 

 
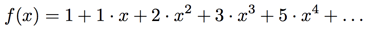
The hope is that, now that we converted the Fibonacci sequence  into a power series  we can use algebra as in the last section to gain additional insight about 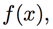 and then translate that back into insight about the sequence 

Consider multiplying by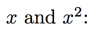 

 
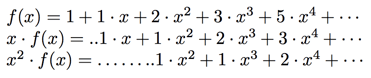
If you look in each column from the bottom up, you will notice that the coefficients of each  term are consecutive Fibonacci numbers. But because each Fibonacci number is the sum of the previous two, that means exactly that each coefficient in the top row is the sum of the corresponding coefficients in the bottom two rows, with the exception of the lone 1 in the first row. That is,

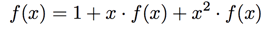
We took the recurrence relation which characterizes the Fibonacci sequence and turned it into an equation of power series! With some further algebraic manipulation, we solve:

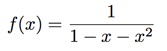
Again, using algebraic manipulation we turned a power series from an infinite sum to a compact expression as a fraction. But we can simplify even further. You may recall the technique of partial fractions: if we factor the polynomial 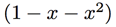 into linear terms  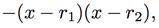we can rewrite the fraction

 
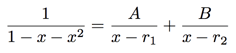
for some numbers A and B.

We will determine these numbers later-- 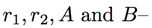but first let's take a step back and ask, why does this help us? Remember, in the previous section we derived a simple expression for the power series given by the fraction  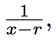namely 

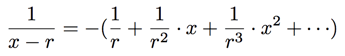
We thus obtain

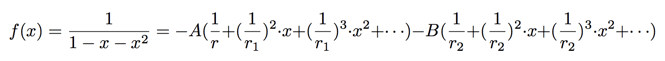
From this, we can read an expression for the Fibonacci numbers. Remember,  is the coefficient of  in the power series  which, by above, is

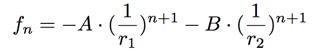
The explicit equation we've been looking for! It now remains to solve for the numbers 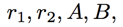 and plug in. This is an exercise in algebra which you are encouraged to solve. I will spare you the details and skip straight to the final answer:

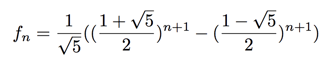
At first glance, this might appear to be a very surprising answer. After all, the Fibonacci numbers  are always whole numbers, and yet our formula above involves the decidedly unwhole quantity  It turns out, however, that whenever we evaluate the formula for a specific value of n, all of the squareroots end up canceling out and we magically obtain a whole number. For example, if we plug in n=0, we get

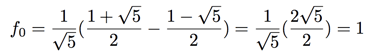
This solution conveys some of the power of generating functions. By converting the combinatorial sequence of interest into a power series, we can use algebra to massage it into a form from which we can more readily read off the coefficients. 

Rate of Growth, Revisited

In addition to the satisfaction of having arrived at an explicit solution for the Fibonacci numbers, the solution also gives us a more precise answer concerning the rate of growth of the Fibonacci numbers.

Let's take a closer look at the solution

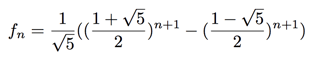
The two instrumental numbers here are 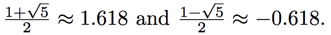 The former is larger than 1 while the latter has absolute value less than 1, so the term  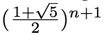increases exponentially while the term  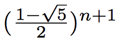decreases exponentially, becoming negligably small for large n. So for large enough values of n, we can approximate 

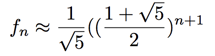
In fact this approximation holds fairly well even for small values of n. This means that the long-term rate of growth of the Fibonacci numbers is 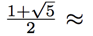approx  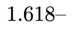each month the population of rabbits is approximately multiplied by this rate. Incidentally, this number is known as the golden ratio, a ratio which has been known since antiquity for cropping up in many geometric constructions, and which is believed to be especially aesthetic, hence "golden." It is this number which drives the hidden engine of the Fibonacci numbers.