I thought that it would be fun to tackle a geometry problem on today's post. I know what you're thinking, fun and geometry – can these two words even go in the same sentence? But yes, geometry can be fun; let's see as we work together through the details of a particular problem.
Without further ado, let’s examine a question that I came across recently:
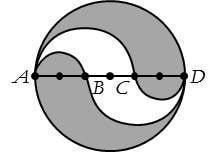
Semicircular arcs AB, AC, BD, and CD divide the circle above into regions. The points shown along the diameter AD divide it into 6 equal parts. If AD = 6, what is the total area of the shaded regions?
(A) 4π
(B) 5π
(C) 6π
(D) 12π
(E) 24π
Yikes, this looks like my worst nightmare from my Geometry course. Can I find the answer to this SAT problem online?
Perhaps your internet search skills are better than mine, but I thought we might be better off tackling this problem with a pen and paper.
What are your tips for solving this SAT problem?
One of the biggest challenges of this problem is to separate the drawing presented above into three separate figures:
- The large circle, INCLUDING #2 and #3 below
- 2 equal white semi-circles (on either side of the diameter), INCLUDING #3 below
- 2 equal small shaded semi-circles (similarly, on either side of the diameter)
Using the numbers above to refer to the areas of all 3 figures, we will solve the problem as 1 – (2 – 3), or the sum of the area of the circle less the area of the white region (the white region defined as #2 less the overlapping semi-circles in #3). The result is the area of the shaded region.
Okay, let’s go!
- The large circle: The total area of a circle with diameter 6 is πr2 = π*(6/2)2 = π*32 = 9π.
- 2 equal white semi-circles: Each semi-circle has a diameter of 4 and a radius of 2. Their combined area is: 2((π*22)/2) =(π*22) = 4π.
- 2 equal small shaded semi-circles: Each half circle has a diameter of 2 and a radius of 1. Their combined area is: 2*(π*12)/2 = (π*12) = π.
- Now let’s take 1 – (2 – 3): 9π – (4π – π) = 6π. The correct answer is C.
Wow! Was that SAT magic?
It might have seemed that way, but it wasn’t. Often the hardest part of solving geometry problems is recognizing the different shapes within a figure (sometimes a collection of rectangles or triangles, or circles as in this problem), separating the figure into its component parts, and solving. Sometimes, your first attempt to create distinct shapes does not work out as planned – perhaps you have too few, or too many, rectangles, for example – but don't let that deter you! Stick with it, and you will find the right combination of shapes to solve the problem.

Comments