Physics problem-solving or: How I learned to stop worrying and love abstraction

Hi, everyone!

I am a physics tutor here at Cambridge Coaching, and I will be blogging tips and tricks for dealing with physics problems.

I’m drawing mainly on patterns I’ve noticed as a college physics tutor, but what works for a freshman mechanics problem set also works in high school, on the SAT 2 and GRE, and in the rest of your college physics courses.  Doing physics is just like learning any other skill set; if you develop good technique when learning the basics, you’ll find that picking up a new skill is no problem!

The great thing about physics is that, at least when you’re first starting out, you’re dealing with real, visible, tangible objects.

You’ve thrown a ball, ridden in a car, and maybe even seen a spherical cow or two.  You know that if you drop a ball straight off the roof of your house, it does not, despite what may come out of the algebra, take 80.9 seconds to land on the lawn. 

This visceral, intuitive connection between the numbers on your paper and the real-world objects in your imagination can be very powerful.  You should never stop asking yourself your answers make physical sense because, after all, we are trying to figure out what happens to real objects in real, if somewhat contrived, situations.

Oftentimes, however, students tend to use this connection to real-world quantities to form a series of numerical stepping stones by which they can hop through a problem.  For example, imagine being told that a cannon fires a shot at 15.0 m/s at 45.0 to the horizontal and being asked to find the maximum height.  We might do the problem like this:

“Ok, we fire the cannon at 15.0 m/s at an angle of 45.0 degrees and we need sine [calculator tap tap tap], so that’s 0.707 times [tap tap tap] 15 is 10.7.  We plug that in for v_i  and we know a is -9.8, so we get d is [algebra algebra tap tap tap] 5.84!  The ball goes 5.84 high, and that must be in meters!”

This approach is like doing the pizza wedge on a ski slope; it will get you down the easier parts of the hill, but you will work harder than necessary and miss out on most of the fun.  Over the next several posts, we’ll go through a few changes you can make to how you approach physics problems that will have you slaloming through your problem sets.

Don’t round too soon in the physics problem!

In the example, we were given three significant figures for each number (15.0 m/s and 45.0 degrees), so we kept three sig figs in each step of our calculation.  Rounding early to 0.707 led us astray, though.  You should only ever round at the end of the problem.  If we had carried all of our digits until the end, we would have found an answer of 5.74 instead of 5.84.

I once helped a student who had struggled for the better part of an hour with a problem.  She couldn’t see where she had made her error, but her answer was consistently slightly different from the answer in the back of the book.  Her understanding of the material was spot-on, each math step was fine, and she had carried all of the digits that her calculator had given her, but she still could not find the few missing hundredths of a meter.  As it turned out, the calculation was so complex that the rounding that the calculator had done to fit the answer into its display had introduced an error that, by the end of the problem, had grown large enough to throw off her answer noticeably.

In the next section, I will describe a problem-solving method that will both make our lives easier and enable you to completely avoid this easy mistake.

Embrace Abstraction

Is there any easier way to do the example problem?  Yes!  If you are trying to set up a pair of new bookshelves in your dorm room (and kudos for scoring a room with space for bookshelves), you don’t put all of your books on the shelves and then arrange the shelves to fit the room – you shuffle the empty shelves around until they‘re exactly where they need to be and then you load them down with your collection.

In the same way, variables are easier to rearrange before they’ve been loaded down with as many digits as you can carry.  In my example, we used the formula

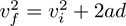
applied in the vertical direction to find the answer but, retroactively carrying all our figures, we came to it dragging along v_i = 10.6066 m/s.

Instead, we should look ahead and figure out where everything will need to go ahead of time.  We know that we want to find d, the distance from the ground to where the ball stops rising, and we know that v_f is zero, so we can do the algebra first to find

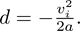
Can we plug in yet?  No, we need the initial vertical velocity and we’re only given the initial total velocity.  That is given by

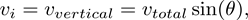
so altogether we have

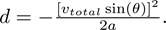
Now, we plug everything into the calculator in one fell swoop and skip all of the intermediate steps we slogged through before.  We never round, so it’s impossible for us to make the rounding error that threw off our earlier answer.

You might say that you’re more comfortable working with numbers the whole way through and that the two methods will yield the same results as long as you’re careful.  You are right, of course, for the simpler problems.  In the same way that rocking the trusty pizza wedge becomes laborious on a moderate ski slope and nearly impossible on a steep run, the method in my example will become more and more difficult to use as you advance in physics.

In the next several posts, we’ll explore ways that staying abstract will help you solve problems more efficiently, state your answers with more confidence, and perhaps even notice a few cool things along the way.