
In our last post, we introduced the concept of dimensional analysis, which involves thinking about the units that are used in a problem. In this post, let’s look at a few instances in which dimensional analysis can be tremendously useful while preparing for a test or thinking through a physics problem.
A great memory aid
Dimensional analysis is a great way to help us memorize formulas. In our test-day freeze-up example, dimensional analysis helped us use our fragmentary and uncertain memory of the formula to arrive at the correct answer.
Imagine how much more efficient studying for the test could be if you accounted for this process ahead of time! Say you need to memorize the oscillation frequency of a pendulum, the period of a mass on a spring, and the speed of a wave on a string for a test. This could be preparation for a high school physics exam, college physics quiz, the SAT 2, or the GRE.
Instead of memorizing the three separate equations, just remember that you are solving for the angular frequency or velocity, and that there are no numerical factors that can trip up your dimensional analysis. On test day, it should take you ten seconds or less to write down the relevant quantities for the situation you need (l and g for the pendulum, k and m for the spring, the tension F and density 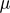 for the string) and rearrange them to find your answer. Does l/g give the frequency or period, again? Don’t memorize; use units!
for the string) and rearrange them to find your answer. Does l/g give the frequency or period, again? Don’t memorize; use units!
After writing down those two equations for the oscillation frequencies of the pendulum and spring, let’s see if any patterns jump out at us. g and k are both on top, and they are related to the restoring force, the force pulling the pendulum or spring back to the middle. l and m are on the bottom, and they are related to the inertia of a system, the quantity that keeps a moving system in motion.
Does this pattern also hold for the third example of the speed of waves travelling on a string? If we imagine a standing wave whose wavelength is equal to the length of the string, what does its frequency look like, and does this fit into the broader pattern?
It seems that, in general, the harder you push a system back toward equilibrium and the lighter the system is, the faster it oscillates. Imagine a very light block oscillating on a very stiff spring; does this make physical, intuitive sense that the block oscillates quickly? Keep this pattern in mind later on when we test our dimensional analysis skills with a real-world example.
Problems of scaling
Dimensional analysis is also a wonderful shortcut for problems that ask about scaling. If we quadruple the length of a pendulum, what happens to its period? Here, we can use dimensional analysis with confidence because even if we missed some numerical factor, that factor would be the same for both lengths and we can ignore it.
So let’s go through the thought process explicitly: The period is inversely proportional to the frequency, so
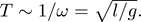
Notice that we’re missing the factor of 2 pi that comes in from relating the period to the angular frequency
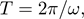
but that doesn’t matter. All we care about is how the period scales with the length, not the explicit relationship. We can see that if the length quadruples, the period should be cut in half!
Let’s take a more complicated real-world example. The pitch of a timpani drum is tuned by pressing a pedal that adjusts the amount of tension on the head, the membrane stretched across the top of the drum. If a timpanist presses the pedal down and doubles the tension applied to the head, how does the frequency change?
First, what are the relevant quantities in the problem? There’s some sort of restoring force, which is given by the tension T on the head. The tension is just a force applied uniformly around the edge of the head, so the correct units are N/m. There is the heaviness of the head material, which can be expressed in terms of 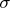 , the mass density per unit area (kg/m2). Finally, there is the radius r of the head, which has units of m.
, the mass density per unit area (kg/m2). Finally, there is the radius r of the head, which has units of m.
By looking at the units, we see that the frequency has to scale like
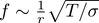 .
.
This quick and abstract problem-solving method obfuscates a lot of interesting details about different modes of the drumhead, but the result is the essential relationship we are looking for. Assuming that the timpanist excites the same drumhead mode before and after tuning, the frequency should go up by a factor of 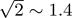 !
!
Developing intuition
Overall, dimensional analysis is a great tool for developing your physical intuition. Learning formulae to prepare for the big test becomes far easier if you can use dimensional analysis to remember where all the factors go on test day. Once you can use your physical intuition to fit disparate formulae into broader, more general patterns, then you will become much more comfortable with physics and a far more effective test-taker.
Comments