Welcome to the last post in our series on experimental error! As a physics tutor, I walk you through the experiental process and explore the traps that might lead you down the wrong path.
Over the last several posts, we’ve explored the concepts of accuracy and precision of a measurement, averaging out the noise inherent in your measurement, and identifying and quantifying any biases that might be throwing your results off.
In this post, let’s put it all together. We’ll return to the experiment mentioned in the very first post and see how all the techniques we have learned enable us to reach our goal: writing down a final result, along with a quantified, rigorous statement of how much certainty we have about that result. The types of skills that these techniques encompass – thinking deeply and analytically about a physics problem, using your physical intuition to brainstorm problems, and applying rigorous analysis methods – will be useful throughout your career, from high school physics classes, through the SAT 2 and AP tests, into college physics courses and GREs, and hopefully beyond.
What result do we want?
Let’s briefly remind ourselves what we’re trying to measure. In this experiment, we are trying to measure g, the acceleration due to gravity, by dropping a ball from a known height and measuring how long it takes to hit the ground. We can solve for g to find
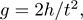
where t is the measured time and h is the measured height from which we drop the ball.
Rule 1: Add or subtract two quantities – add absolute errors
The height h is the more straightforward quantity. Say we know the top of our table is 1.403± 0.002 m from the floor and we hold the ball 0.540 ± 0.010 m above the tabletop. We can measure the table height to a precision of 2 mm but our arms can only hold the ball to within 1 cm of the intended drop height.
This brings us to our first rule of propagating errors: When you add two quantities, you add their absolute errors. This makes intuitive sense if you imagine trying to measure a room by laying many cheaply made yardsticks end to end; if each yardstick might be independently off by, say, a tenth of an inch, then all those many tenths of inches will add up to give you the uncertainty in the length of the room.
If the total height is given by
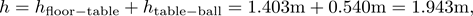
then the total uncertainty in the height is given by
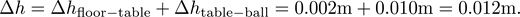
Rule 2: Multiple or divide two quantities – add relative errors
Let's step away from the ball-dropping experiment for a moment to introduce rule 2. Say you want to multiply the velocity displayed on your car’s speedometer by the number of hours spent listening to a carefully selected iTunes playlist to find the number of miles covered in your roadtrip. In this case, you need to take another approach to propagating errors. When you multiply or divide two quantities, you add their relative errors.
The reasoning behind this rule is also easy to understand. Say you drive for 4 hours at 65 miles an hour, but traffic and rest stops put uncertainties in both your velocity and time: you weren’t doing 65 the entire way (traffic), nor were you on the road for the full 4 hours (rest stops). Because velocity and time are multiplied, the absolute uncertainty in terms of miles caused by your rest stops depends on your average velocity, and the absolute uncertainty caused by traffic depends on your total travel time. Consequently, it’s hard to determine what your total absolute uncertainty should be. If, on the other hand, you say that your travel time is 4 hours plus or minus 10% and your velocity is 65 mph plus or minus 15%, then you can say that the total distance traveled is 260 miles plus or minus 25%, or 260 ± 65 miles.
More generally, if
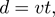
then the total relative uncertainty is
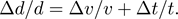
Rule 3: Raise a quantity to a power – multiply relative error
Now that we’ve seen rule 2, rule 3 is straightforward to understand. Let’s circle back to our ball-dropping experiment to see it applied. By using the techniques outlined in the previous posts, we can come up with a statistical uncertainty (from our noisy measurements) and a systematic uncertainty (from biases in our experiment) for t. The total uncertainty in t, then, is just the sum of the two:
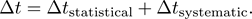
Notice, though, that our expression for g depends on t2, not t. In the same way that raising a number to the nth power is equivalent to multiplying that number by itself n times (i.e. 23=2*2*2=8), when you raise a quantity to the nth power, you multiply its relative uncertainty by n.
Bringing it all together
Now, we can apply all three rules to figure out the uncertainty we should quote for our final answer. We find
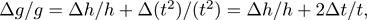
and, plugging in,
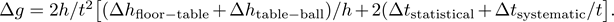
And so concludes our analysis of the ball-dropping experiment! It is a relatively simple experiment, one that most physics students see in the first few weeks of their high school class, but we have hopefully illuminated some of the subtleties that arise when performing even such a straightforward experiment.
Comments