 Having worked through a long physics problem, you finally have an answer. How do you know if it’s right and all that work wasn’t for naught? In this post, I will cover a few quick strategies that can help rule out wrong answers.
Having worked through a long physics problem, you finally have an answer. How do you know if it’s right and all that work wasn’t for naught? In this post, I will cover a few quick strategies that can help rule out wrong answers.
We will use the following problem as an example:
A motorized toy car of mass M = 504 g rests on a table and is attached by a string to a post at the center of the table so that it can move in a circular path with radius L = 1.1 m. The motor causes it to travel with a constant velocity so that it is undergoing uniform circular motion about the post. The string has a maximum tension Tmax = 10.2 N at which it will break. What is the maximum velocity that the car can achieve without breaking the string?
Work through the problem with variables
One simple strategy that you can try from the very beginning of the problem is to work to the solution using only variables and not values given in the problem. There are several benefits to this strategy. The first is that it is easier to go back and check for algebra errors with variables as opposed to numbers. If an error has been made, this will make it easier to pinpoint and correct it. The second benefit is that computed values are much simpler to check because all numerical calculations are at the end. This means that the actual computation only needs to be verified at the end rather than throughout the problem. Additionally, because the numbers are all plugged in together at the end, rounding errors can be avoided because rounding is only done once rather than being distributed throughout the problem.
For our example problem, we will start by recognizing that the tension, T, provides the centripetal force, Fc. The centripetal force can generally be expressed as:
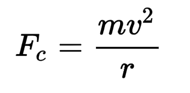
In this equation, m is the mass of the object, v is the velocity, and r is the radius of the circular motion. For the toy car in our equation, if we plug in our specific variables with T = Fc, we are left with the following equation:
Solving for the maximum velocity gives:

Order of magnitude
Once you have calculated your answer, you should consider whether your result is reasonable or not. You should try to get a sense of the values of different quantities in SI units. This can be challenging for Americans because we do not use the metric system but it is an important skill to develop. For instance, it’s helpful to know that if a baseball pitcher throws a ball at 1 m/s or 1000 m/s, these rates are probably unreasonably slow and fast, respectively. You may want to remember approximate conversions between SI and units you are more familiar with, if that is easier. For instance, a meter is approximately equal to a yard.
We can now plug in our example problem: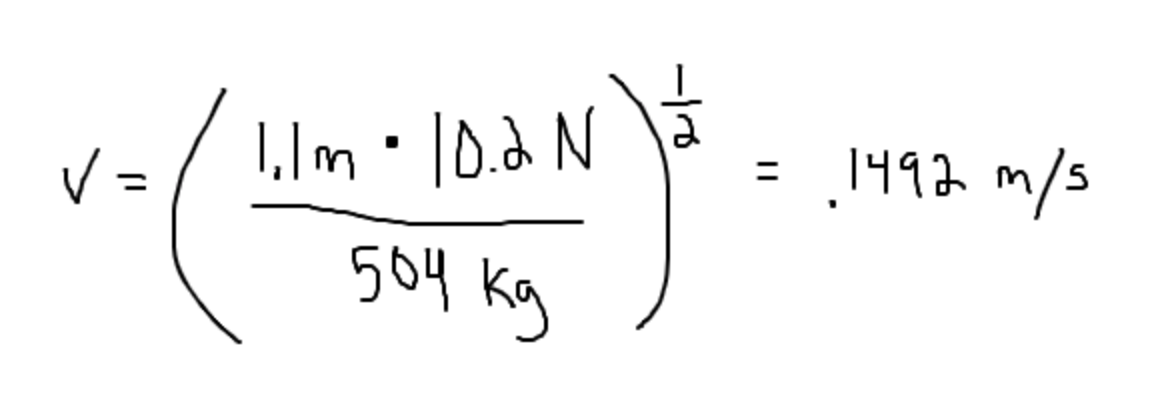
After plugging in these numbers, our answer seems like a relatively slow velocity for such as small car. This should be a hint to check what we plugged in! Notice that the problem gave the mass in g instead of kg, so we know that we plugged in the wrong number. The true value is thus the following:
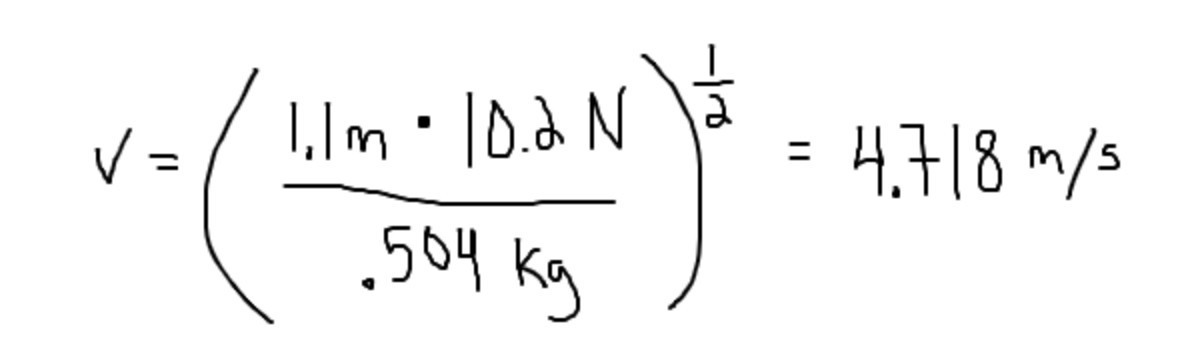
This seems like a more reasonable value. Note that initially solving the problem using variables makes checking that we plugged in the correct values a one-step process rather than a multi-step one tracing through the whole solution.
Significant Figures
While not a method for checking solutions, it is still important to remember to check your significant figures. Some tests remove points for the wrong number of significant figures, so be sure not to lose easy points!
In this problem, the length of the string is only given to two significant digits, which limits our solution to only two significant digits. We should round so that v = 4.7 m/s.
Units
It is always important to include the units in the solution. It is typically easiest to solve problems using only SI units but there will be cases where this is not true. Whatever units you use, make sure that you are being consistent throughout the entire problem. For example, if you choose to use liters for volume instead of cubic meters, make sure you do so for every quantity in the problem. I typically list all the known values given by the problem at the top of my page where I am solving the problem. This is the point at which I convert to the units that I will be using to solve the problem so that I don’t forget later.
For the example problem, I would list L = 1.1 m, T = 10.2 N, and M = .504 kg. The only quantity that needed to be converted was mass, which was given in g in the problem. Note that this would have helped avoid the mistake we saw earlier.
Dimensional Analysis
Dimensional analysis is one of the most powerful tools for checking an answer and relies on verifying that the units of the solution are correct. For example, we know that any solution for acceleration must have units of m/s^2 if SI units are used. Dimensional analysis highlights algebra errors because this typically causes the units not to work out correctly. To use this technique, all units should be converted to SI base units like kilograms, meters, and seconds. For instance, a joule is equal to a kilogram meter squared per second squared.
Our solution for the car's maximum velocity is:

If we plug in the units of L, Tmax, and m, we find:
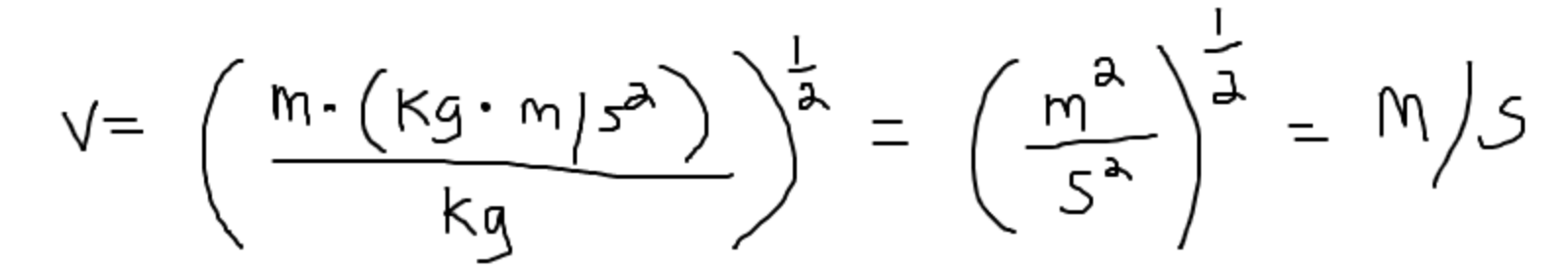
And this is correct! If we had made an algebra error and found the incorrect solution, we would not find units of m/s and would know to check our solution.
Taking limits
An additional benefit to finding your final answer in terms of variables is that it allows you to take limits. You can check whether the solution makes sense by looking at the effects of increasing or decreasing terms in the solution. This requires some physical intuition and is a skill that you will build as you solve more problems. Useful limits tend to be 0 and infinity for most quantities. For angles, 0 and 90 degrees tend to be useful limits as they reduce cosine and sine to 0 or 1.
We found the following solution for our example problem:

Let's examine the effect of the three parameters in the solution on v. First, notice that v increases as T increases, as it is in the numerator. This makes sense because the car should be able to move faster if the cord is stronger. We also notice that v increases as L increases. This also makes sense because the longer the cord is, the less sharp the turn is and the less force is required from the cord to turn the car. Lastly, notice that v decreases as M increases. We would expect this because the more massive the car is, the harder it is for the cord to cause it to turn. This should cause the cord to break at a lower velocity. Our solution seems reasonable from taking limits.
Final Thoughts
It is always important to make sure that your answer to any physics problem is reasonable. Take advantage of these techniques to avoid and catch algebra and computational errors. Implementing an organized approach to problem-solving will help you solve problems correctly with more consistency. With practice, these techniques will become second nature and will help you verify that your solution is the correct one.
Comments