
Whether you have struggled in your math classes or have excelled so far, to ace the new SAT math section will require putting in additional work. You will need to set aside time to practice for it.
Time is a major factor in the math section, so obtaining the highest score will require more than simply being able to figure out a way to get to the right answer—it will often necessitate being able to identify the quickest way to get there.
As beautiful a mathematical mind as you might have, it will take you longer on average to reason through a problem that you haven’t seen before than to solve a problem very similar to one you have already worked through. Once you’ve practiced enough, you will be able to recognize patterns in how certain questions are asked that will allow you to solve those questions quicker and more accurately.
Example 1
Suppose that you see the following problem:
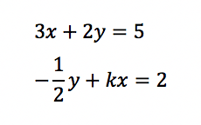
The pair of linear equations above has no solution, and k is a constant. What is the value of k?
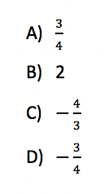
If you are a little rusty, it may take you some time to arrive at the correct answer. Or you may be stumped altogether. But after practice, you will quickly be able to parse what the questions is asking. You will instantly recognize that when the question describes the two equations as being linear that means that when graphed in the x-y plane, each equation will depict a line. And you will know that two of the most important characteristics of a line are its slope and its y-intercept, which is why the SAT loves to test your ability to rearrange equations to get them into slope-intercept format. It will also be old news to you that when an equation is written in slope-intercept form (y = mx + b), it becomes easy to quickly glance at the equation and ascertain what the slope and y-intercept are. And you will be able to recognize in your sleep that the coefficient of the x term (represented by the letter m) is the slope, and that the constant, b, is the y-intercept, or the y-value when the line crosses the y-axis. Furthermore, through practice you will be able to quickly identify that a solution to a set of linear equations is the point at which they intersect, so if the equations have no solution that means they describe parallel lines.
Since parallel lines have the same slope as each other, this is the key insight necessary for solving the problem. You can now rearrange each equation so that it is in slope-intercept form, and then set equation one’s slope (m1) equal to equation two’s slope (m2).
1.
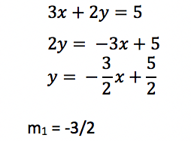
2.
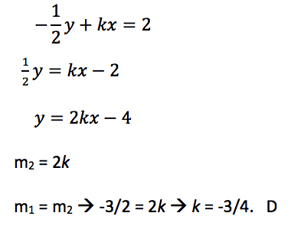
Being able to quickly recognize this type of problem will allow you to solve it fast, without having to spend precious time up front thinking about what it means for a pair of equations to have “no solution.” Practicing this type of problem will also help you recognize common variants of it—such as if the prompt had described the pair of equations as having infinite solutions or if it described the lines as being perpendicular to each other.
Example 2
In the triangle below, what is the length of side b?
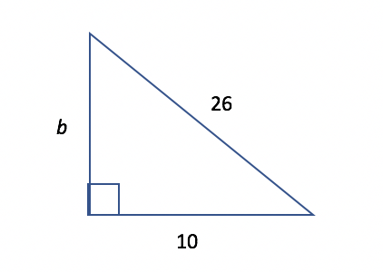
If you remember the Pythagorean theorem then you know that for a right triangle, ![]()
. You could plug in the lengths of the triangle into this formula and solve for the missing side, b, to arrive at the right answer. In a homework assignment for math class, this is a perfectly good approach.
However, in this example it is not the quickest approach—and therefore it is not the optimal one for the SAT.
Special Right Triangles
There are certain combinations of lengths of the sides of a right triangle that the SAT is most likely to ask about. If your goal is to ace the SAT math section, you should commit these special combinations of right triangle lengths to memory. Specifically, 3-4-5 triangles and 5-12-13 triangles are ones that you are most likely to be asked about. Once you memorize these combinations, you will be able to immediately recognize the missing length if you are given a right triangle with two sides that correspond to either of the above combinations.
If you see:
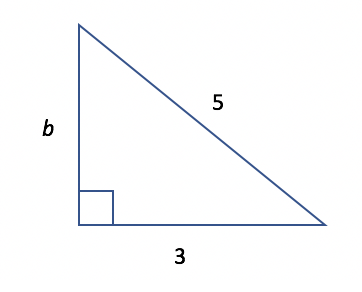
then you will instantly recognize that this is a 3-4-5 triangle and that b must be the missing value of 4, without having to square any numbers, use any algebra, or solve any equations.
Once you memorize the 3-4-5 and 5-12-13 right triangle combinations, you will also be able to recognize the missing length of any right triangle that has side lengths that are each a particular multiple of these special triangles. For example:
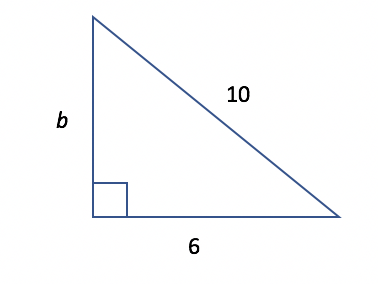
in this triangle, two of the known lengths (6 and 10) each reflect a multiple of 2 times the lengths of two of the sides in a 3-4-5 triangle (i.e., 3*2 = 6; 5*2 = 10). Therefore, we can solve for b as being two times the length of the missing side in a 3-4-5 triangle (b = 4*2 = 8).
Knowing this, we can return to the problem earlier:
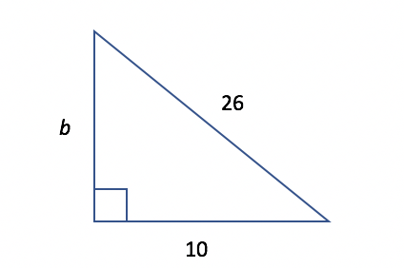
You will now recognize that the two known sides (10 and 26) each reflect twice the side lengths of a 5-12-13 special triangle. Therefore, b must equal twice the side length of the missing side (b = 12*2 = 24).
Tricks of the Trade
We’ve just covered two specific examples of test-taking strategies that you can use to ace the SAT math section. There are many more strategies that will help you save time and identify the correct answer quicker. Practice makes perfect, so start preparing as soon as you can!
Sign up with me or one of the other experts at Cambridge Coaching to work on additional strategies for acing the SAT math section!
Want to learn more about the SAT? Feel free to browse our SAT section of the blog!

Comments