Step 0 – Make Sure the product makes sense!

Say we’re given two matrices A and B, where

and we’ve been asked to find the product AB. To see if AB makes sense, write down the sizes of the matrices in the positions you want to multiply them. In this case, we write

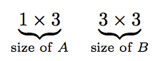
To check that the product makes sense, simply check if the two numbers on the inside agree. If they do, the product can be taken, if they don’t agree, the product doesn’t make sense. For instance, even though the product AB makes sense, the product BA does not. Indeed, the inside numbers of

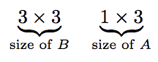don’t match up.

Step 1 – If the product makes sense, find the dimensions of your answer

Again, we can make use of the technique of writing down the dimensions in order. Let’s take the same A and B from above. We write down

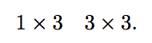
The outside numbers, in order, give the dimensions of the product. Reading the outside numbers left to right, we get 1 × 3, which is the dimension of

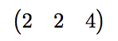
or the product AB. We’ll compute this ourselves in a minute! To recap,

• Write down the dimensions of the two matrices A and B. 

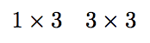
• Check if the inside numbers agree.

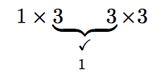
• If they agree, read the dimensions of the answer off the outside numbers

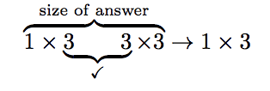
Special Case – Multiplying a row vector by a matrix

Step 2 – Write out the rows of the matrix on the right

In our example, we would write

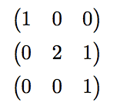
Make sure you write them in the order they appeared!

Step 3 – Multiplication

Multiply the first row of B by the first entry of A, the second row by the second entry, and so on.

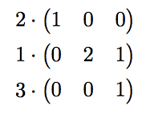which equals

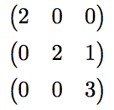
Step 4 – Addition

Add up the rows you got in step 3 to get your answer

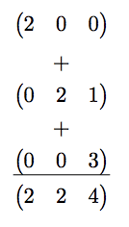
General Case -- Two Matrices

Now let's say we want to multiply a new matrix A' by the same matrix B, where

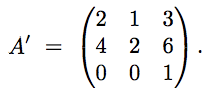
Doing steps 0 and 1, we see

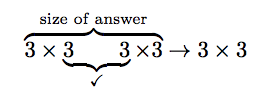the product makes sense and the output should be 3 X 3.  We'll find the output row by row.

Step 5 – Break both matrices into rows

In our example, we would write

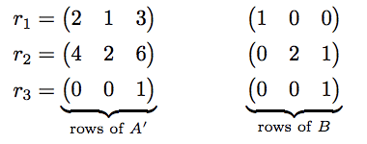
Step 6 – Repeat Steps 1-4 for each row of A'

To find the first row of our 3x3 answer, compute the product , the first row of A' times B.

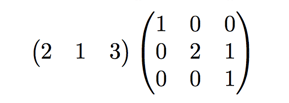
which is the problem we just solved. So, the first row of our answer is

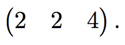To find the second row of our 3x3 answer, compute , which I'll leave the reader to verify is 

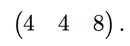
Finally, the third row of our 3x3 answer is , so we multiply

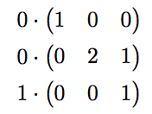and then add

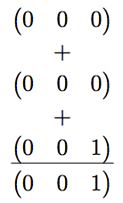
We've found the three rows of our solution matrix and we conclude

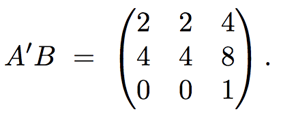
The common way of stating this perspective is that in the multiplication of AB, A acts on B by row operations. We view B as a collection of row vectors and the rows of A have us take linear combinations of the row vectors in B to form the rows of the solution. There is an equivalent perspective of column operations. Each has their place. Stay tuned for a follow-up post about how each of these perspectives comes into play when solving the matrix equation Ax = b.

Are you interested in connecting with a mathematics tutor like Jesse?