Equations in math are useful but they’re also kind of inefficient – for each x value, you have to do a separate calculation to figure out what y is. Graphs take that equation and turn it into a visual, something you can look at and immediately see what happens at different values of x, how the function changes, and more!
However, when you first learn graphs it’s all about memorizing basic equations and what their graphs will look like, starting with the slope-intercept form of linear equations. However, as you move on to trickier equations like quadratics and trigonometry, you’re often asked to memorize forms of equations like these –
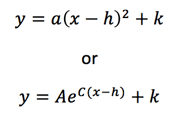
- where you have to memorize the exact equation setup and what each term means on the graph, whether it’s the vertex, slope, intercepts, scaling, horizontal or vertical shifts, or more!
But why memorize all those a’s, c’s, k’s, and h’s if it’s only going to be useful in a few specific cases?!
Instead, the next time you need to know what a graph of a function should look like, try these steps to quickly sketch out any graph!
To demonstrate, we’re going to use the equation:
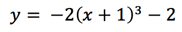
It looks similar to polynomial equations you may have seen in class, but it’s cubic, so we don’t have any obvious equation forms to use to set up the graph. So, how do we graph that function?
1. Plot x = 0
The first thing we want to do is get some points up on our graph, so we want to pick the ones that will be easy to calculate. For almost any equation, plugging in x = 0 and solving for y is fast and easy to do by eye, and almost always doable without a calculator. For our example equation:
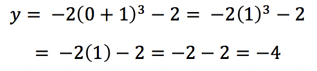
So, the first point we’ll put on our graph is (0, -4).
a. If you can easily find it, plot y = 0
Next, in some cases, y = 0 is pretty easy to solve for too. If you can solve for y = 0 quickly, it’s another good point to solve for right away. In this case:
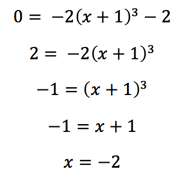
So, now we have point (-2, 0) to add to our graph!
b. Bonus: plot a few easy to calculate points like x = 1 & x = -1
Depending on the graph, it might be easy to plug in small integers like 1 or -1. The more points you can add to your graph, the more you can see what shape it will eventually take. However, stick to points that are easy to calculate. The purpose of this method is to find just a few points quickly – if you’re going to calculate every point on the graph, you aren’t saving yourself any time!
For this equation, we’ll get:
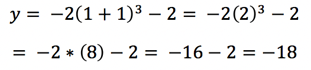
and
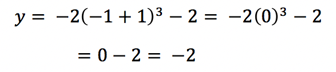
So we now have four points: (0,-4), (-2,0), (1, -18), and (-1, -2). Let’s plot these points and see how they look!
We can start to see the graph take shape, but we’ll need more info before we’re done.
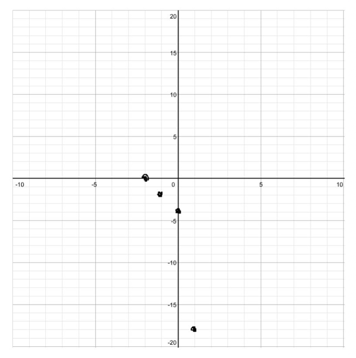
2. Figure out what happens when x is really big (in the positive and negative direction)
Whatever line we draw is going to have to end with arrows at both ends, to let us know what happens as we go further along the x-axis both in the positive and negative direction. This is what’s called “end behavior”. To figure out what it is, we’re going to plug two numbers in to our original equation – a big positive number and a big negative number. Now, we’re not actually going to pick a number and use our calculator to find what happens, we’re just going to see how the parts of the equation will affect the end result.
For example, plugging a big positive number in our cubic function will get:
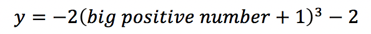
Adding 1 to a big positive number will barely change it - then, when we cube it, it will become a really big positive number.
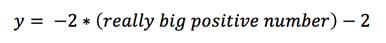
However, a really big positive number will become negative when multiplied by -2, and subtracting 2 won’t make much of a difference so the end result will be a really big negative number.
If we try the same thing for the other side of the graph, plugging in a big negative number for x, we will get:
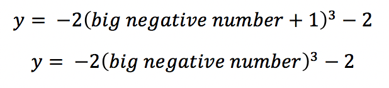
A big negative number cubed is a really big negative number – but this time when it’s multiplied by -2 it will become a really big positive number.
o, for our graph, we found that at large positive x, y is large and negative, and at large negative x, y is large and positive. Let’s add that to our graph with arrows.
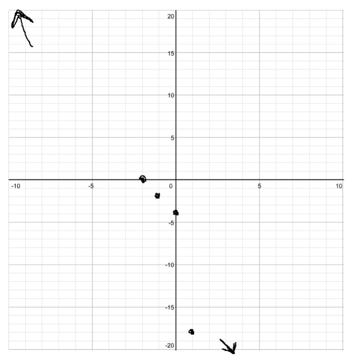
3. Optional: look for any “significant” x-values
Some equations have unusual features or special points that you can spot by looking at the equation – pay attention in particular for any points where a big part of the equation could become zero. This could help you find roots, asymptotes, or other places where the shape of the graph changes in an unusual way.
For example, with the equation we’ve been looking at,
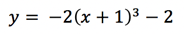
That 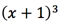 term is interesting because if x = -1 the whole portion of the equation will become zero. Of course, we already found that point earlier, but this tells us that x = -1 is a “special” point in the equation – it’s possible that the shape of the graph will shift somehow here.
term is interesting because if x = -1 the whole portion of the equation will become zero. Of course, we already found that point earlier, but this tells us that x = -1 is a “special” point in the equation – it’s possible that the shape of the graph will shift somehow here.
4. Connect the dots and finish!
At this point we’ve done all we can – we have a few points on the graph, we know what it’ll look like at the ends, and we’ve identified any unusual points or features. We might not know exactly what they are, but we’re ready to draw something.
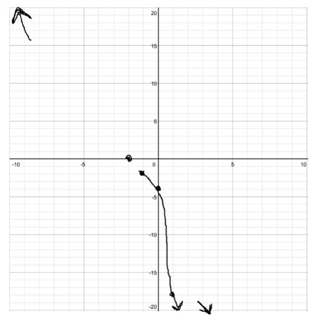
Now, we still might not know exactly what the shape of the graph is, but here you can use the basics for each main equation. We know that our line is going to be smooth and as simple as possible while still hitting all our points. If we know generally what kind of equation it is (polynomial, radical, exponential) we have at least some guess what the general shape would be.
For our example, we have enough points to sketch out one side of our equation, but the negative side is a bit unclear, so let’s think about what we can say about another type of polynomial, the quadratic equation.
For our cubic function, we know that quadratic functions are always symmetric around their vertex, but that doesn’t quite work because we know that in one direction we’ll end up positive, and the other we need to go negative.
So, let’s guess something similar – maybe our “special” point at x = -1 is like a vertex, but at that point the shape of the graph is the same, but moving in the opposite direction. (I’ve put a dashed line down at x = - 1 for reference, but of course that wouldn’t be part of the real final graph.)
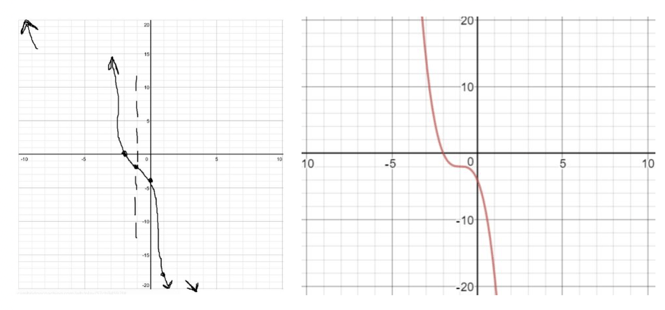
Here we go! It’s not a perfect graph, but in a few quick steps, we at least know in general what this graph is going to look like. In case you’re wondering, here’s what this equation looks like when it’s graphed by a computer.
This method works for a massive range of functions – polynomials, radicals, exponentials, logarithms, trig functions, and more! Just be careful once you get to functions with multiple y or terms: in those cases, the graphs will be unusual, complex shapes, so graph lots of (x, y) points before trying to connect all the dots!

Comments