 In elementary and middle school, we learn mathematics for the sake of mathematics, we are never told what mathematics can ultimately be used for or why mathematics is useful other than the fact that it can help us make change and do our taxes one day. What they should be telling you is that the laws of the universe are written in a language that people are capable of understanding and that this language is mathematics.
In elementary and middle school, we learn mathematics for the sake of mathematics, we are never told what mathematics can ultimately be used for or why mathematics is useful other than the fact that it can help us make change and do our taxes one day. What they should be telling you is that the laws of the universe are written in a language that people are capable of understanding and that this language is mathematics.
1. Algebraic Mechanics
The incredible thing about describing the universe through mathematics is that it not only allows us to describe things we have seen but it also allows us to take those observations and project them into the future. An example of this ability to accurately forecast events is called projectile motion or rocket science (no big deal). A simple example of this is used to describe the path a cannon ball will take when fired out of a cannon. Consider the below illustration:
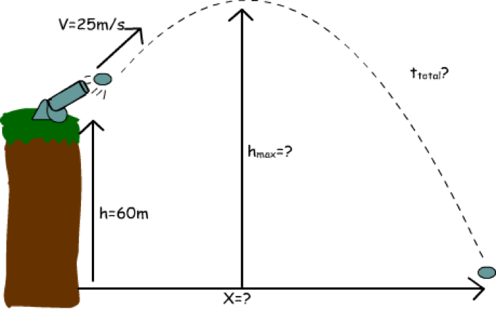
If we are given the starting velocity of the ball and angle of the cannon it just takes some basic algebra/trigonometry to solve not only for the final resting position of the ball but also its position in space at any time following its release. This come about by using the fact that in physics we can treat any two orthogonal directions (at 90 degrees with each other) as independent. Therefore, we can write the equations for the x-position (shown above) and y-position (up in the picture) of the cannon ball and then we will know everything there is to know about the ball for all of time. For those interested these equations are:
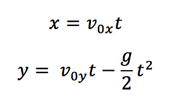
Where x/y is the position in the x/y-direction, v is the initial velocity in the x and y direction depending on the subscript, g is the acceleration of gravity which on earth is about 9.8 meters per second, and t is the time. The two velocities can be found using the sine (for y-direction) or cosine (for x) of the firing angle times the total velocity. Therefore, using these two simple equations we can describe the motion of a cannon ball through space (with just algebra). Adding mathematical tools like calculus and differential equations allows us to expand our methods of describing the universe beyond what most people would think is possible.
2. Conservation Laws – A Tool for Physicists
Now given the last example it is easy to think, “well how did you come by these equations for the cannon ball and can we derive equations like this for a general problem?” The answer to this question is yes and how can be explained using every physicists' favorite tool, conserved quantities. Formally a conserved quantity, let’s call it “qconst” is defined as:
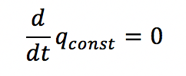
This is just calculus talk for saying that this quantity does not change with time. In other words, if we measure this thing (for example the number of jellybeans in a jar) then no matter when we measure it we will always get the same amount. This in incredibly useful because there are several quantities in nature that are guaranteed to ALWAYS be conserved. An example of one of these quantities is momentum which is defined as:
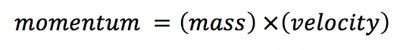
An example of this being useful for physics is the case where two objects collide with each other. Say we have a pool ball sitting motionless on a pool table and you hit this ball with a second ball of the same size. The total momentum before and after the collision (since momentum is conserved) is therefore represented by the equation:
![]()
Where v#start is the starting velocity for each ball, which as we mentioned before is zero for ball number 2 and v#end is the end velocity for both balls 1 and 2, respectively. The m’s in the equation represent the mass of the balls and are in the first equations because of the definition of momentum and disappear after the arrow because we can just divide both sides of the equation by m (algebra). This tells us that if we know the starting speed of the moving ball and the end speed of just one of the two balls we can calculate the speed of the second ball. Using other conserved quantities, we can calculate the end speed of both balls but that is a conversation for a later post.
Another interesting example of momentum conservation is to consider being an astronaut stranded in space motionless and you need to travel forward a few feet to get back to your space ship. What do you do? You cannot garb or push off anything to move forward and it appears it is impossible to move forward those few feet. Well if you are an astronaut that knows about momentum conservation then you would know that all you need to do is take a tool off your trusty tool belt (or anything heavy) and throw it as hard as you could in the opposite direction of your space ship. Since you and your tool both started with zero velocity and therefore zero momentum when you throw the tool you are giving it momentum, therefore to ensure that there is still zero total momentum (because the total momentum is conserved) you must now have the same amount of momentum in the opposite direction. This means by throwing your wrench away from the ship you are now slowly moving (because you are heavier than the wrench) back towards your ship. Momentum conservation saves the day!
3. Relativity- Mathematics Beyond Common Sense
Up until the early 20th century physics used mathematics as a way to model the things people saw every day and acted as a way to confirm the common sense and intuition of scientists. This all changed with the development of special relativity and quantum mechanics, which took cutting edge mathematics and used it to predict properties of nature that were not only difficult to observe, but also that completely defied common sense and the logic at the time.
Special relativity was developed by Albert Einstein in an effort to describe one of lights strangest characteristics, which is that the speed is light is constant regardless of the speed of the observer. In order to understand how strange this is let’s do a quick thought experiment (Einstein loved those). Picture yourself in a car on the highway going 60 mph and another car is driving next to you also going 60 mph. If you ignore your surroundings and only focus on the other car it appears the other car isn’t moving at all and it is as though both you and the other car are just sitting stationary. This probably makes sense to you and this property of motion has been understood since ancient times.
Now picture yourself again in a new very fast car that can go close to the speed of light and you are chasing a wave of light. The intuition we just gained in the last thought experiment says that when we look at the light it should appear to be moving very slowly because we are chasing it at such a similar speed. However, experiment after experiment shows that this isn’t the case and no matter how fast you move you will always observe light to be moving at the same extremely fast speed.
This inconsistency bothered Einstein and he used the most modern math at his disposal to derive general relativity, which explains this phenomenon as well as the nature of all movement in the universe.
What makes general relativity so interesting is that it states that time itself is not a constant of the universe but instead depends on the speed of the individual observing it. In other word the faster you move the slower time moves. This leads to the famous twins paradox. Say you have two identical twins and twin number 1 stays on Earth while twin number 2 gets in a space ship traveling the speed of light. When twin number 2 returns to Earth he/she will now be significantly younger than his/her twin (how much younger depends on how long he/she was traveling close to the speed of light). This to most of us would make absolutely no sense and seems like something out of a science fiction movie (example Planet of the Apes). However, special relativity has proven to be one of the most successful scientific theories in history and is used every day in satellites that enable everything from GPS navigation to the cell phones in our pockets. This is one of the many examples of mathematics leading to an understanding of the universe that goes beyond basics human intuition or logic.
4. Closing Thoughts
Mathematics is a tool that not only allows us to model and predict things we observe in nature, but it also allows for the discovery of new phenomenon beyond the current limitations of our time. This is how we are able to describe objects smaller than any microscope can see and learn about planets we can never travel to. This is what makes mathematics so special, because it is not a language that we created to communicated amongst ourselves, but instead it is a language that we discovered to uncover the secrets of how our universe works.
For more on this subject check out the YouTube channels below:
A quality description of interesting physics ideas (like relativity!)

Comments