Math Tutor: 4 Easy Steps to Volume Rotation Integration

math

By Eriene Sidhom

Merry Christmas Eve! Why yes, I do believe volume rotation integration is as easy as apple pie!

Every once in a while something you learn in class really just knocks you off your feet. Those of you who have taken AP physics will know that position is the integral of velocity. About a month ago, on a fairly dreary Boston morning, I was sitting in my neurobiology class, semi-interested, when the professor informed us off something truly shocking: our brain determines and maintains our eye position by literally integrating velocity information into position information.

It took humanity all the way until Newton and Leibnitz to figure out calculus, and it takes the education system about twelve years to teach calculus. All the while you are subconsciously integrating every second that you are awake. So while it is completely understandable that AP Calculus can be intimidating, it’s at least somewhat comforting to know that you—or at least your eyeballs—have been doing it your entire life!

Unfortunately, as a math tutor near MIT, I’ve found that even for ambitious students, doing calculus is much more difficult. So here are 4 easy steps to remember when doing those pesky volume rotation integration problems.

Problem:

Here’s a pretty basic problem which you may come across in your AP calculus class:

Find the volume of the shape created by rotating the curve y=-x² + 4 around the x-axis for 0<x<2.

So, step 0, is to draw the relevant portion of the graph and figure out the boundaries. Here, I’ve done this one for you:

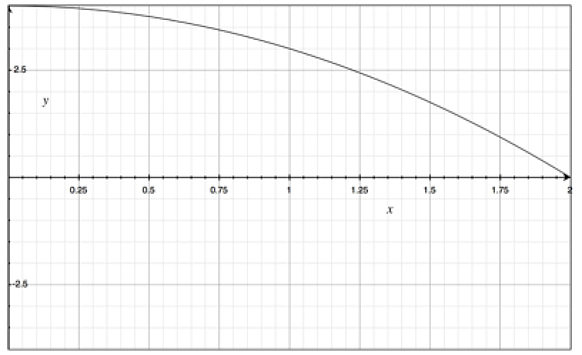
Sidhom_1212014

As you can see, you are rotating the piece of the graph in the upper right hand quadrant. You can imagine, that by rotating around the x axis, you will make a sort of pointed cone-like figure on its side. Now let’s get to the math!

Approach:

Find the easiest shape

Remember the concept of integration is to divide the shape into tiny cylinder-like slices that you will sum together. The height of the cylinder will either be “dx” or “dy”, and the face of the cylinder will be dependent on the slice. So you can either slice the shape horizontally or vertically.

If you slice it horizontally you will end up with half-circles (ending on the y-axis), but if you slice it vertically you will have full circles, since you are rotating around the x-axis. The equation of a circle is pretty easy, so that seems like the better option.

Also, imagine drawing a vertical line through the figure, it crosses the x-axis. This means that the height of each slice is “dx,” thus the variable we integrate will be “x.” This is convenient, since our equation is in terms of x.

Describe the equation

Once we rotate, and divide it vertically into many tiny cylinders. The first step is to find the volume of each of these:

In general the volume of a cylinder is: (Surface area of the circle)*(height).

The height is dx. The surface area of a circle is pr², making the volume of each slice: pr²dx.

Now if we were to sum all these infinitesimal cylinders that gives us an integral. The boundaries are in terms of x: [0,2], so a rough draft of our equation is:

It is easy to see that the only thing we need to figure out now is r.

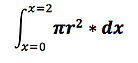
Find the coordinates

The radius of a circle is the distance from the center to the boundary. Since we’re rotating around the x-axis, we know the x-axis is our center. The boundary is determined by y-coordinate on our curve. So the radius of each circle is going to be y-0 or just y.

Consider any coordinate on the graph, (x,y). We can rewrite y in terms of x based on the equation given: (x, -x²+4). Thus for each x between 0 and 2, the radius of the circle is –x^2+4. Substituting into our equation, we have our completed integral:

Below, is a picture that summarizes the previous three steps:

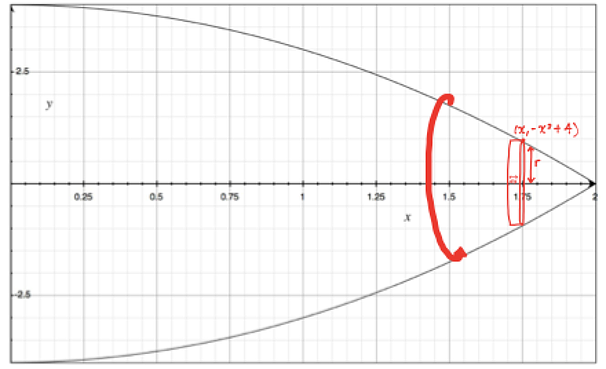
Sidhom_1212014_2

Solve!

Now your integral is a simply polynomial that you can integrate using rules you’ve already learned.

Summary:

While integrals can be intimidating at first, remember the key is to 1) find the easiest shape, 2) to remember the equation, and then 3) to find the appropriate coordinates to substitute into your equation. If you remember these basic steps, you will soon love calculus as much as these fellas. For more inspired reading, check out this blog post on following your math intuition, and translating words into equations, written by an MIT math tutor. For more help with calculus or any other advanced math tutoring needs, consider working with a Cambridge Coaching’s MIT math tutors in Boston, New York, or online.

Did you know we offer tutoring for all subjects?

Learn more

Comments