Triangles can be very different!

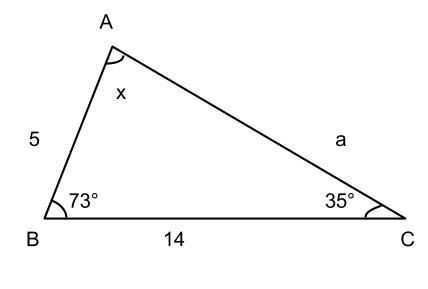
Triangles are the most basic 2D shape that you can create and they can be found everywhere. So let’s look at some tricks and facts about triangles. We’ll start by looking at the triangle below (not drawn to scale).

1) The angles of a triangle

Fact 1: The angles of a triangle add up to 180°.  This fact you just have to drill into your head. It’s a specific case of the general rule that the angles of a shape with n sides add up to 180(n-2), but even if you forget that, keep the number 180° in your head. With that fact, we can then deduce that angle x is 72°:

73° + 35° = 108° → 180° - 108° = 72°

2) The third side of a triangle

Fact 2: The third side of a triangle is greater than the difference of the other two sides and less than the sum of the other two sides.  A question that might show up on a geometry test is one that asks you for a possible length of the third side. Taking the fact above, we can find the lower and upper bounds:

14 - 5 = 9

14 + 5 = 19

Thus, side a must be between 9 and 19.

3) Angles and the side across from them

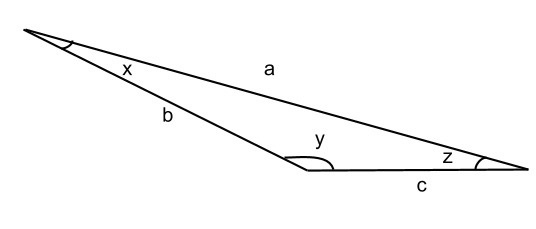
Fact 3: The angles of a triangle are proportional to the sides across from them.  What does this mean exactly? This means that the bigger an angle is, the bigger the side across from it is, and vice versa. So just eyeballing the triangle above, it might be hard to tell if side a or b is longer. But because we can see that angle y is clearly the largest angle, we can infer that a is the longest side. Angles x and z look fairly similar, but since side b is visibly longer than side c, we can infer that angle x is the smallest.

Use facts like this to help you infer information about a triangle if the question does not say “Not drawn to scale.”

4) The same angles

Fact 4: If two triangles have the same angles, their sides are proportional to each other.

5) If two triangles are parallel

Fact 5: If the sides of two triangles are all parallel, then their angles are equal. These two facts refer to what are called similar triangles. Similar triangles have the same angles and are thus proportional to each other. Observe the triangle (not drawn to scale) and the problem below:

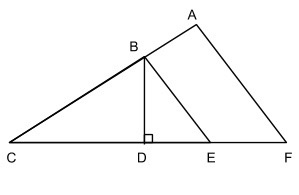
AF = 10, BE = 8, BD = 5, and CF = 15. AF and BE are parallel. What is the area of triangle BCE?

First, let’s label the diagram. Because we need to find the area of triangle BCE and we know that the height is 5, we need to figure out the base (CE). So let’s label the diagram, calling CE x, since that is what we want to solve for in order to find the area of the smaller triangle:

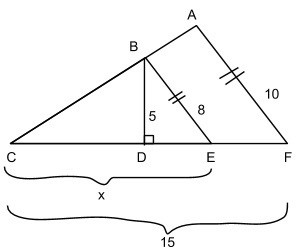
We use double lines to mark lines AF and BE as parallel. Fact 5 can be invoked here because if two lines overlap, they must be parallel. Thus, since CE and CF overlap and AC and BC overlap, they are also parallel. Therefore, triangles ACF and BCE share the same angles and are therefore similar triangles. Whenever you see any two triangles drawn overlapping like in the diagram above, you can immediately recognize them as similar triangles.

So, let’s use Fact 4 now. You can either set up the proportion as:

Big side 1    Small side 1 10 8

-------------      =    ---------------- → ---- =        ----

Big side 2    Small side 2 15            x

OR:

 Big side 1    Big side 1 10 15

---------------- =   ----------------- → --- = ----

Small side 1  Small side 2 8 x

Remember that the parallel sides must be either horizontal (as in the first case) or vertical (as in the second case) to each other. In the first equation, the bigger triangle’s side AF (10) is horizontal from the smaller triangle’s side BE (8). In the second equation, it is vertical from the smaller one.

Both equations will yield 10x = 120 and therefore x = 12.

We can then multiply this base 12 by the height 5 and divide by 2 (remember: a triangle’s area is ½ * base * height (= bh/2) to yield the area of triangle BCE as 30.

Remembering Special Right Triangles

Beyond the basic equilateral, isosceles, and right triangles that you should remember, there are two key right triangles to memorize. These are the 45/45/90 triangle and the 30/60/90 triangle. Let’s look at the former first:

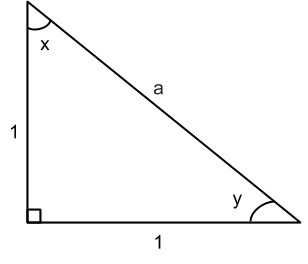
Using fact 3 from above, we know that angles x and y must be the same, since the sides across from them are equal. Since they must add up to 90°, each one must be 45°:

90° + x + y = 180°

x = y

90° + 2x = 180°

2x = 90°

x = 45°

y = 45°

Now, what is side a? We can use the Pythagorean Theorem, remembering that a is the hypotenuse:

12 + 12 = a2

2 = a2

a = √2

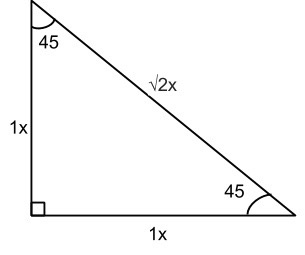
45/45/90 triangles show up often on geometry tests and it’s important to remember that they will always be in the following ratio because they all share the same angles (remember Fact 4 above):

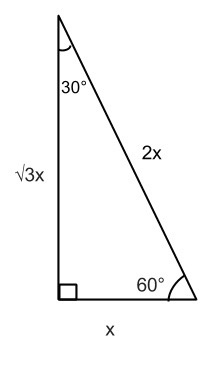
Now let’s take a look at a 30/60/90 triangle. These triangles lie in a 1, √3, 2 ratio.

It’s relatively easy to remember the sides of these triangles: the trick is to count up from 1 and square root the highest number.

1. For the 45/45/90 triangle, you know both equal sides have to be the smallest and so they are both 1. Count up to 2 for the hypotenuse and square root that. So a 45/45/90 triangle is in a 1:1:√2 ratio.

2. For the 30/60/90 triangle, all three sides have to be different since angles are different. So counting up from 1 and square rooting the highest number will give you 1, 2, √3. But which side is which? Because √1 is 1 and √4 is 2, we know that √3 has to be the middle number, so it has to be across from 60° and 2 must be the hypotenuse as it is the largest number. The ratio then is 1:√3:2.

Finding Triangles in Bigger Shapes

Armed with these triangle tricks, we can solve what initially seem to be daunting problems. Take a look at the following problem (again, not drawn to scale):

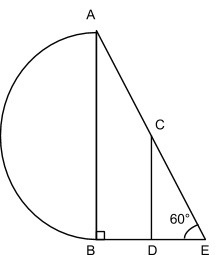
If the area of the semicircle from A to B is 13.5π, CD is one third the length of AB, AB is parallel to CD, and angle CED is 60°, then, what is the area of triangle CDE?

So it seems at first that we have very little information, but let’s work on this systematically, going through each piece of information.

1. Let’s use the first piece of information, that the semicircle’s area is 13.5π. Notice that AB is the diameter of the semicircle. What would the area of the full circle be? Just double it and you get 27π. From that area, we can work backwards to get the radius:

πr2 = 27π

Divide by π: r2 = 27

Square root both sides: r = √27

Factor it: r = √27 = √9 * √3 = 3√3

Now, the radius is half the diameter, so double it to get the diameter. 6√3 is the length of line AB.

2. CD is one third the length of AB, so it is 6√3 divided by 3 = 2√3.

3. AB is parallel to CD and we see that AE and CE overlap and that BE and DE overlap. Therefore, the two triangles are similar and angle CDE must also be a right angle (like angle ABE).

4. Angle CDE is 60°, so we therefore have a 30/60/90 triangle! Let’s redraw the diagram with the information we’ve gathered.

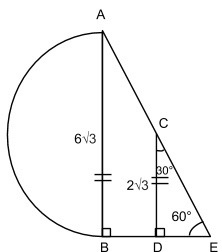
5. We have the height of triangle CDE (2√3) so now we just need to find the base (DE). Remember 30/60/90 triangles are in the ratio of 1:√3:2, so:

2√3    √3

-----    =    ----

DE      1

Cross out √3 in the upper terms and you get that DE = 2. For good measure what is the length of CE? It’s twice DE, so it must be 4.

6. Now we can apply the triangle’s area formula (bh/2)

2 * 2√3

----------- = 2√3

       2

By now, you should be a master of triangles! When you see what looks like a complicated geometry problems, use these math SAT section tips and always look for triangles (and other familiar shapes like rectangles and circles) to use each piece of information step by step in order to get the information you need to solve the problem.