 Pure Algebra is not the most efficient way to solve every problem!
Pure Algebra is not the most efficient way to solve every problem!
After spending some time working in the Official GMAT book, you may have noticed that many of the math problems can get pretty complicated. Perhaps you struggled with a harder problem and finally had to check the back of the book for the solution, only to find that the solution is literally over half a page of complicated algebra. How are we expected to solve such a problem in two minutes? How would we not run out of time?
For many of the questions, the purely algebraic route does not make a ton of sense. On Problem Solving especially, it can often be much more efficient and strategic to “work backwards” by picking test numbers and “plugging in.” Let us consider the following example. First, we will make an attempt to set it up algebraically.
Official Guide 2020: Problem Solving #199
During a trip, Francine traveled x percent of the total distance at an average speed of 40 miles per hour and the rest of the distance at an average speed of 60 miles per hour. In terms of x, what was Francine’s average speed for the entire trip?

Let’s consider the first statement, “Francine traveled x percent of the total distance at an average speed of 40 miles per hour.” We can represent this as
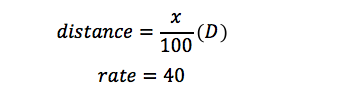
Now let’s consider the second part of the statement, “and the rest of the distance at an average speed of 60 miles per hour.” We can represent this as
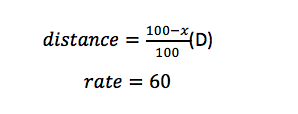
Now, let us consider what the question is asking for: the average speed for the trip. We will use the following formula:
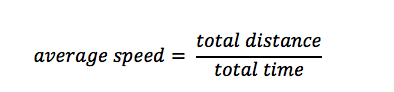
We know the total distance for the trip is D. The total time for the trip would be the time for the first portion plus the time for the second portion. Here, we can use
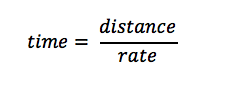
To calculate the time of the first portion, we divide the first distance by the first rate
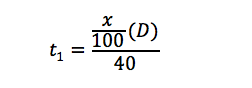
To calculate the time for the second portion, we divide the second distance by the second rate
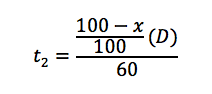
The total time would now be:
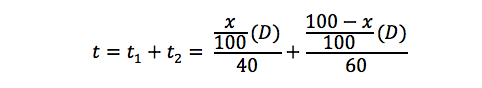
Now, we plug everything into the average speed formula:
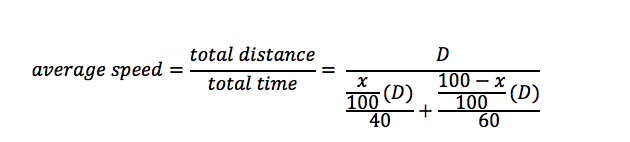
In theory, if we simplify this algebraic expression, we will get one of the answer choices, but this seems like a lot of work! Instead, we can pick test numbers for D and x to see if we can narrow down to one of the answer choices. I will pick:
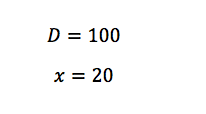
And now we plug in!
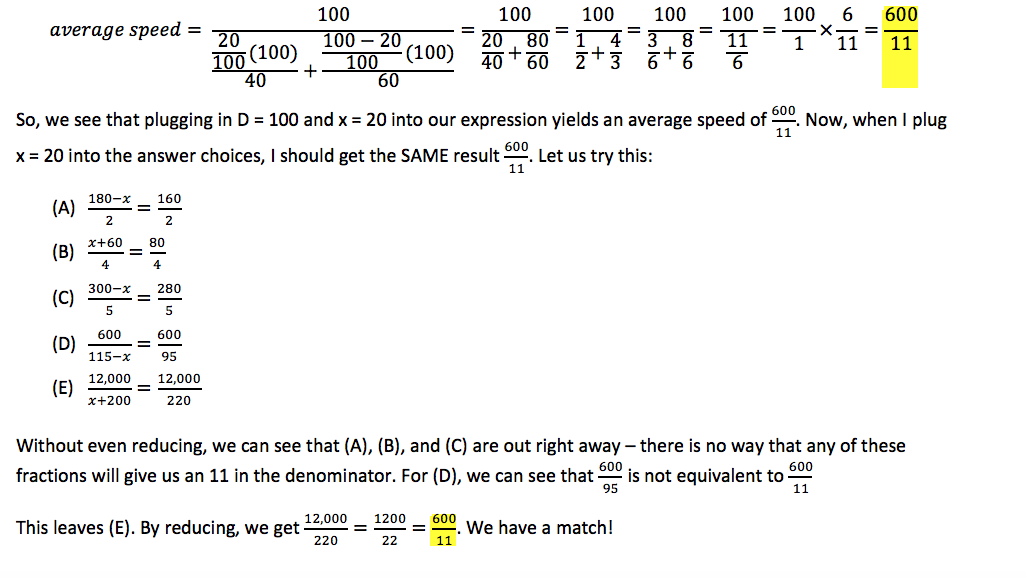
*As a side-note, x = 20 is not necessarily the nicest test number (x = 40 would have been an even easier test case. Feel free to give this a try to see what I mean), but I wanted to demonstrate that this technique still works effectively - even if we get weird fractions.
So you are saying that I should avoid algebra and just pick test numbers for every question?
Definitely not! Algebra is the most efficient way to solve many GMAT questions. In some cases, picking test numbers can actually be more work than simply doing the algebra. We should always make an attempt to set up the question algebraically. It is only when the algebraic simplification gets overly complicated that we should consider switching to a “test numbers” strategy. Consider the following case:
Official Guide 2020: Problem Solving #167
Four extra-large sandwiches of exactly the same size were ordered for m students, where m > 4. Three of the sandwiches were evenly divided among the students. Since 4 students did not want any of the fourth sandwich, it was evenly divided among the remaining students. If Carol ate one piece from each of the four sandwiches, the amount of sandwich that she ate would be what fraction of a whole extra-large sandwich?
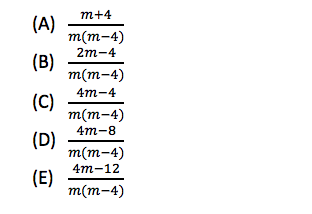
Let’s try to get an algebraic set-up first. We start with the first statement, “Three of the sandwiches were evenly divided among the m students.”
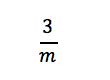
Moving onto the second statement, we learn that four students did not want the fourth sandwich, so it was divided among the remaining students (i.e. 1 sandwich was divided among the m – 4 remaining students)
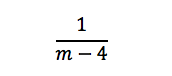
Since we know Carol ate a piece from all four sandwiches, we can represent what she ate by writing:
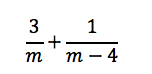
Now we have a decision to make. Either the algebra is straightforward enough to proceed with simplifying the expression, or the algebra looks too complicated and we pick a test number for m. In this case, assuming we know how to add fractions by finding a least common denominator, algebra will be much faster.
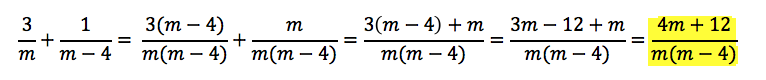
The answer is (E).
Picking numbers would have worked too, but we would have had to test all five cases. This could potentially take much longer than simply adding the two expressions algebraically.
Okay great. So, sometimes I should use algebra, and sometimes I should pick test numbers. How do I decide which to do?
This is one of the most common GMAT questions I get. My advice is this:
- Assume algebra. Start by setting up the question algebraically. This will also help you better understand what calculations you will need to do in the problem.
- Try to simplify as much as you can algebraically
- If things start getting messy and complicated, consider switching gears. Work backwards from the answers or pick test numbers to see if you can narrow down to one answer choice.
How will I know when the algebra gets too complicated?
This largely depends on your personal comfort level with algebra. My strategy is typically to stick with algebra until I get confused or bogged down by the complexity of the equations. If I feel myself getting lost, I switch to “testing numbers.” Furthermore, I already have an algebraic set-up where I can plug in my numbers.
In conclusion
As you prepare for the GMAT quant section, recognize that there are multiple ways to solve many of the problems. You can do pure algebra, you can work backwards from the answer choices, or you can try to pick strategic test numbers. Your method will largely depend on your comfort-level and familiarity with the math concepts. That said, it can be really instructive to solve each problem multiple ways – that way, you can decide for yourself which method is the most efficient for you.
Alex grew up in the suburbs of Boston and attended Harvard University as an undergrad, double-majoring in mathematics and music, and spending his spare time music-directing and accompanying productions for the Harvard-Radcliffe Drama Club. After college, Alex went on to pursue his Master’s degree in Musicology at Oxford University, where he researched Chopin’s use of harmonic progressions. Currently, Alex works full time as a math and standardized test preparation tutor. He has successfully helped students reach their academic goals for over six years.
Alex firmly believes that teaching is about being adaptable, and he tailors his teaching style to students’ individual needs. He also recognizes that taking a standardized test can be very daunting for many people, and he fosters a non-judgmental setting where students feel comfortable asking questions. At Cambridge Coaching, Alex’s area of specialty is the GMAT and GRE. He also has extensive experience tutoring high school and college-level math up through single-variable calculus.
Taking the GMAT in 2020? Check out some of our previous blog posts below!
When should I guess on the GMAT?

Comments