Sometimes, when you are sitting in a physics class staring at an intimidating wall of math, it can be easy to lose sight of the fact that the laws of physics originated as hypotheses to explain observations in the real world. Whether it was Newton getting bopped on the head by an apple, Galileo dropping stuff off the Tower of Pisa, or Franklin electrocuting himself with a kite, there was often an experiment that preceded and informed the mathematical formulation of a physical law. As a physics tutor in Cambridge, I find that it’s easier for my students to stomach the math if they’re able to imagine what it means, if they can figure out the physical consequence hidden behind the equation. For example, when looking at Newton’s second law (F = m a), I imagine pushing on a box. When I push (apply a force) on the box (a mass), it starts moving (it accelerates). If I push harder (apply a larger force) on the box (still the same mass), it starts moving more quickly (a larger acceleration). And while thought experiments are great, real experiments are more fun! Today we will set up some experiments to investigate one of the more abstract concepts in classical mechanics: the moment of inertia.
What IS inertia, exactly?
Inertia is one of those quantities that kind of makes sense when you first hear about it, but then the math starts getting complicated and physical insight can be obscured. Basically, inertia is a measure of how difficult it is to rotate an object around a particular axis. The more inertia something has, the more torque is required to get it rotating – you can think of inertia as the rotational analogue to mass. As you might imagine, the geometrical shape of the object matters, as does the position of the axis of rotation. Intuitively it is clear that rotating a rod that is fixed at one end is somehow different than rotating a rod that is fixed at its center, one case is likely to be harder than the other.
So, what is the real-world consequence of this? What does it mean physically that some objects are harder to rotate than others? What does it mean that the geometry of the object matters? Let’s try to set up a situation in which having different values for the inertia creates different observable outcomes. The simpler the experiment, the better, because it will be easier to understand the results. Why not just get a bunch of different objects and start rotating them around! Whichever one is most difficult to rotate must have the largest moment of inertia. However, this doesn’t seem to be a particularly good experiment – “this one feels harder to move” isn’t a very precise measurement. Another idea is to find a bunch of different objects and roll them down a ramp! The objects will be rotating as they roll down the ramp, so the inertia is likely to influence the outcome. For simplicity, we can limit the experiment to objects that have a circular cross-section. We will have a clear way to measure the results: which object gets to the bottom first?
The Experiment
First let’s pick some objects that are easy to get a hold of, so that you can try this for yourself if you like: we’ll start with a marble and a pool ball. They both have the same geometry – both are solid spheres – but their mass and size are quite different. Let’s see what happens!
The race is on! Here is the view from the starting line.
Here is the view from the finish line.
It looks as though the two balls cross the finish line at the same time! This is perhaps somewhat unexpected; most people think the pool ball should cross first because of its larger size and mass. Let’s try to figure out what’s going on here. As with many mechanics problems, the simplest way to analyze this situation is to use conservation of energy. At the top of the ramp, each object has some potential energy due to the gravitational force. At the bottom of the ramp, that gravitational potential energy is converted into kinetic energy – some of the initial potential energy is used to get the objects rotating, and some is used to move the objects down the ramp. So our energy balance equation will look like this:
(initial potential energy) + (initial kinetic energy) = (final potential energy) + (final kinetic energy)
We know that the objects start from rest, so the initial kinetic energy is zero, and we know that at the bottom, the objects have zero potential energy. Also, we can split up the kinetic energy into the energy due to rotational motion and the energy due to linear (or ‘translational’) motion:
(initial potential energy) = (final rotational kinetic energy) + (final linear kinetic energy)
Now we dig into our bag of formulas and fill out the equations with variables. We’ll use the subscript m to refer to the marble and the subscript p to refer to the pool ball:
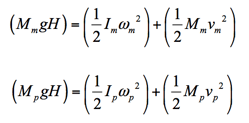
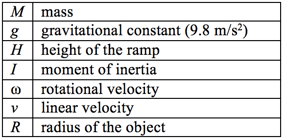
There are a lot of variables in there, so here is a table to keep track of them all:
Now, since both balls start from rest, whichever ball has the most linear speed at the bottom of the ramp will be the one to cross the finish line first.* Using the formula for the moment of inertia of a sphere rotated about its center, and rewriting the rotational velocity in terms of the linear velocity, the equations become:
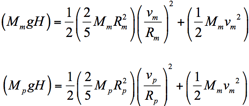
It looks like the mass and the radius cancel out! Simplifying the equations, we have:
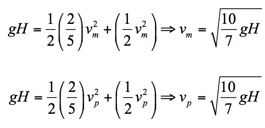
As we can see, the marble and the pool ball have the same velocity at the bottom of the ramp, which explains why they cross the finish line at the same time. What did we learn here? The math says that the two objects should get to the bottom at the same time, and that is indeed what we observe. But why is this the case? The mass and size are different for the two objects, but those quantities get canceled out in the energy balance equation, and do not influence the result. However, the geometry of the objects is the same – they are both solid spheres. So, this suggests another experiment: taking two objects with different shapes and repeating the race! By comparing the results of the two experiments, we will be able to build some intuition about rolling motion.

Comments