The power of prime factorization for the GMAT quantitative section

We have all encountered factor trees at some point during grade school. When I first encountered them as a kid, the whole exercise seemed unnecessary and silly. I thought to myself, “Great. I can list all the prime factors of 48. But, to what end?” It was not until much later that I realized the utility of prime factorizations. On an exam like the GMAT, where we are expected to do some pretty big calculations without a calculator, finding a prime factorization can be clutch.

Wait. What is a prime number again? I barely even remember what factors are!

Remember that a factor is any integer that divides evenly into another integer. For example, 7 is a factor of 21 because 7 divides evenly into 21. Also, remember that a prime number is any integer whose only factors are 1 and itself. For example, 13 would be a prime number because its only factors are 1 and 13. The number 15 would NOT be a prime number because 1 and 15 are not the only factors; 3 and 5 would be factors as well.

The smallest prime number is 2, and the first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 23, 29…

Okay cool. So, why do I care about finding prime factors?

A prime factorization is like having the DNA for any integer. Let us consider the Prime Factorization of 990:

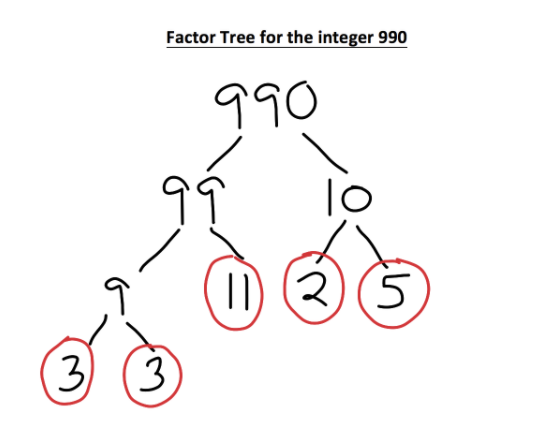
We also know which numbers are definitely NOT factors. For instance, the number 14 CANNOT be factor. Since 14’s prime factors are 7 and 2, we would HAVE to have a 7 in our prime factorization for 14 to be a factor.

In short, a prime factorization tells us all the factors (and non-factors) of any integer.

Finding the Greatest Common Factor (GCF) and the Least Common Multiple (LCM) of any two integers

We can use prime factorizations to find the Greatest Common Factor (GCF) and the Least Common Multiple (LCM) of a pair of integers.

The GCF refers to the largest integer that can divide evenly into both numbers. Let us consider the following example.

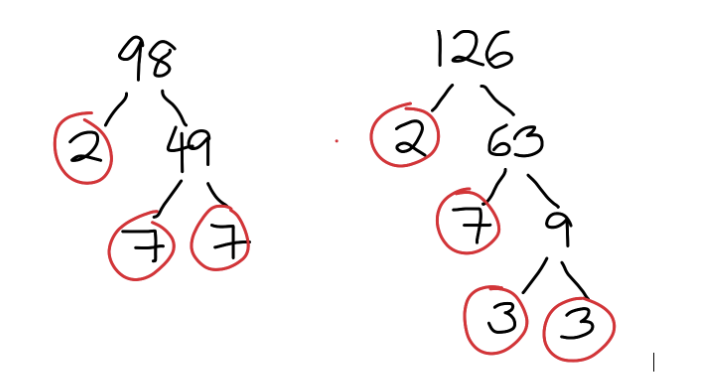
Example 1: Find the GCF of 98 and 126

First, we find the prime factorizations of each:

Example 2: Find the LCM of 66 and 84

Again, we start with a prime factorization of both numbers:

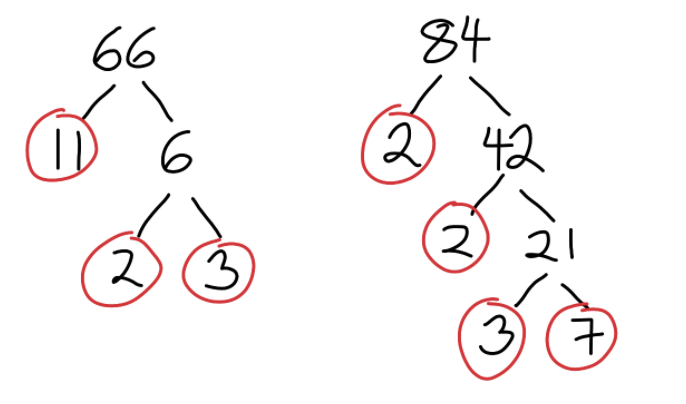
We get the following:

66 = 2 · 3 · 11

84 = 2² · 3 · 7

Now, we ask ourselves what is the least integer that "contains" both of these prime factorizations? To fit 66, we need at least 2, 3, and 11. If we want to fit 84 in, we will need an additional 7 and additional 2 (to make it 2²).

The LCM of 66 and 84 is 2² · 3 · 7 · 11 = 924

Got it. So, how can I apply my prime factorization skills on the GMAT?

Let us examine a GMAT problem together to see how prime factorizations can be helpful.

Official Guide 2018: Problem #195 from p. 175 of GMAT Official Guide 2018 (copyright 2017 by the Graduate Management Admission Council, published by John Wiley & Sons, Inc., Hoboken, NJ)

If y is the smallest positive integer such that 3,150 multiplied by y is the square of an integer, then y must be

(A) 2

(B) 5

(C) 6

(D) 7

(E) 14

First, we “translate” the statement, “3,150 multiplied by y is the square of an integer.” We will use n to represent the integer.

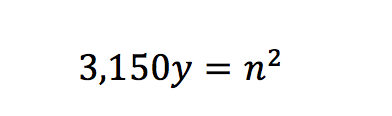
Now let us find the prime factorization of 3,150:

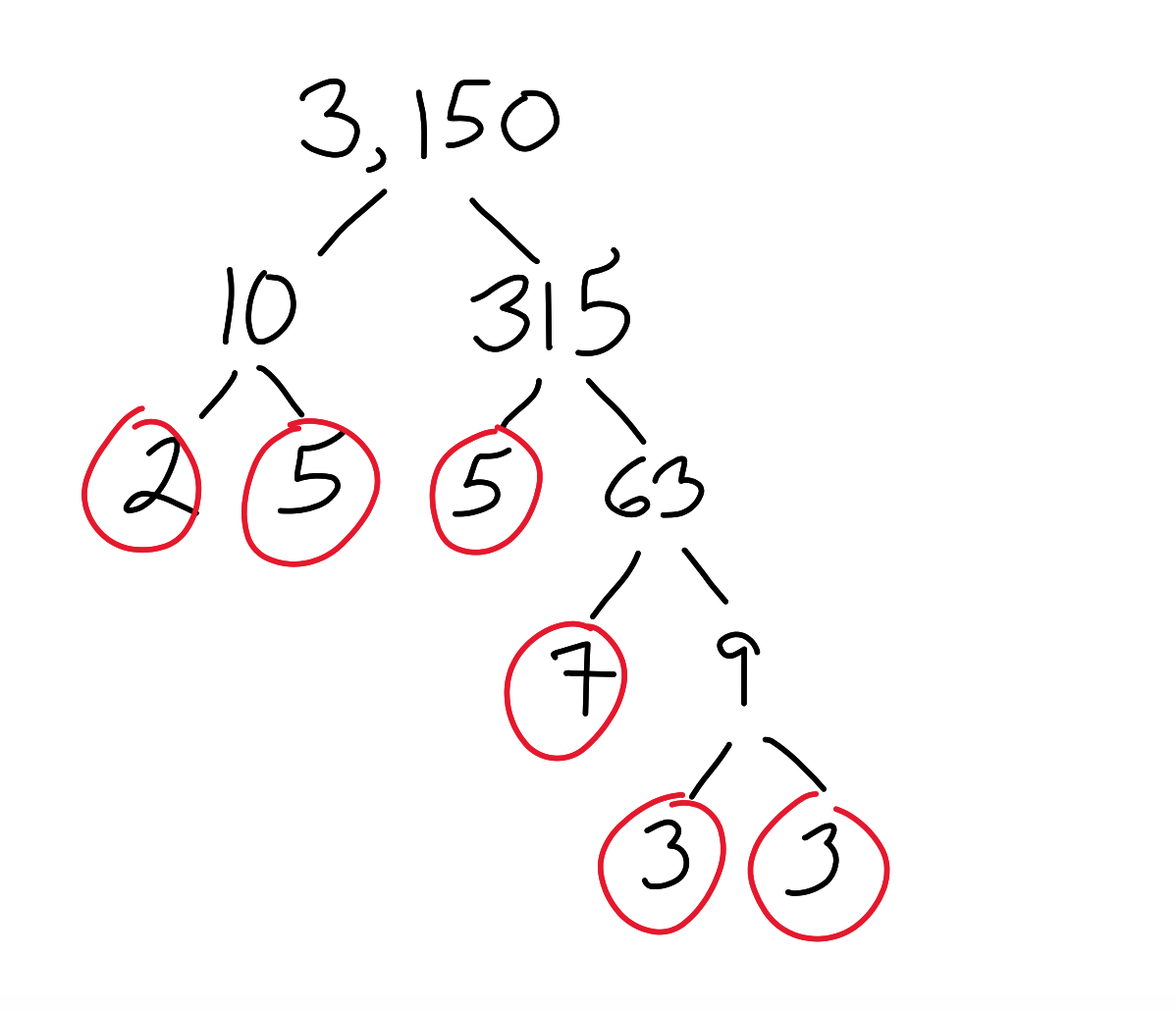
We get 3,150 = 2 · 3² · 5² · 7. Let us plug this into our original equation:

3,150y = n²

(2 · 3² · 5² · 7)y = n²

Now, let us consider what we know about the prime factorization for a squared integer. For an integer to be a perfect square, the prime factorization must contain all even exponents. This fact should be clear if we consider just a few examples.

36 = 6² = (2 · 3)² = 2² · 3²

144 = 12² = (2² · 3)² = 2⁴ · 3²

225 = 15² = (3 · 5)² = 3² · 5²

Squaring an integer requires us to double every exponent; therefore, all our exponents will be even. For our original problem, we need to find out the minimum value of y such that the prime factorization of n² will consist of all eleven exponents. In other words, we need another 2 and another 7 to make 2² and 7².

If we make y = 2 · 7 = 14, then:

2 · 3² · 5² · 7 · y =

2 · 3² · 5² · 7 · 14 =

2 · 3² · 5² · 7 · (2 · 7) =

2² · 3² · 5² · 7²

We have a squared integer! Therefore, the minimum value of y must be (E) 14.

In conclusion

Integer properties are a big deal on the GMAT, and finding a prime factorization is one of the most useful tools for dealing with these question types. A full understanding of factors and multiples of integers will help you gain some ground on the GMAT quant section. As always, be sure to keep track of any GMAT problems you miss during practice, and look for patterns in the question types you miss the most frequently – this is the best way to study and improve your score.