Mathematical induction is a common and very powerful proof technique. At its core, it’s an appeal to an intuitive notion that Induction proofs often pop up in computer science to prove that an algorithm works as intended (correctness) and that it runs in a particular amount of time (complexity). In this tutorial, we’ll break down a classic induction problem in mathematics, and in the next post, we’ll apply the same techniques to a classic computer science problem.
As a warmup, we can look at a classic example used to teach induction, namely the proof that the sum of integers from 1 to n is equal to:
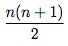
There are two aspects to any induction proof...
Base Case
This is where you try to show that the thing you’re trying to prove in general works for a specific case.
Here a simple case is to show my formula works if n = 1. Let's plug this into our formula:
[n(n+1)] ÷ 2 = [1(1+1)] ÷ 2 = 1
And that makes sense! Often times the base case is generally plugging in what you know/a relatively simple case where your statement holds true.
Inductive Case
This is the ”meat” of the argument. Here we want to show that if I assume my formula/statement works up to a point (call this point k) then it must work for a point up to (k + 1). The key part here is that we are assuming the thing we’re trying to prove already works up to k. Hence we can freely use the result we’re trying to demonstrate and the burden of proof is on us that our formula holds true for the next case.
Going back to our example, we will assume that our sum formula holds up to k, namely the sum from 1 to k satisfies
Our ultimate goal is to show that the formula holds true for k + 1.
At this point, creativity comes into play. How might you start going above building up the next case from the previous case? In this instance, we might suspect that a good way to start would be to add k + 1.
Let's assume that the sum from 1 to k is equal to:
Now, we'll examine what happens if we add k + 1. Adding it we get the following:
Now, for ease of seeing, let’s just set k+1 = k'. Now we have the sum from 1 to k' equal to the following:
Which is exactly what we tried to prove! (note that the variables k, k', etc are arbitrary). Stepping back, what have we shown?
We’ve shown that if my formula holds for a point 1 to k I can show you that my formula will hold for k + 1. In my first base case, I’ve also shown you that I know my formula works for k = 1. Combining this with the inductive step, I’ve shown that my formula points up to k = 1 then it holds for k = 1 + 1 = 2. But by the same logic, I’ve shown that if k = 2 is true, then I can show you it holds for k = 2 + 1 = 3. We can do this ad nauseum and we’ve, therefore shown that our original formula works for any positive integer n. See how we never had to go for every single case (integer) to prove this formula, it was sufficient to show how to build up from a smaller case (k) 2 to the next, larger case (k+1). This in general is a very powerful and common computer science technique used in algorithm techniques like divide and conquer. For the computer science example, we’ll take a look at mergesort and how to show that it’s correct. The questions to ask are 1) What is my base case and 2) what is my inductive step.

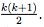
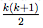
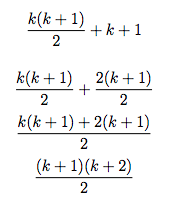
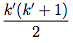

Comments