.png?width=1080&name=Statistical%20Mediation%20%26%20Moderation%20in%20Psychological%20Research%20(12).png) For many people studying for the GMAT, Work/Rate/Time problems prove to be a particularly sore spot on the Quantitative Reasoning section. In this lesson, we will learn an efficient and effective way to tackle these problem types algebraically.
For many people studying for the GMAT, Work/Rate/Time problems prove to be a particularly sore spot on the Quantitative Reasoning section. In this lesson, we will learn an efficient and effective way to tackle these problem types algebraically.
Work/Rate/Time problems are based on one simple formula.
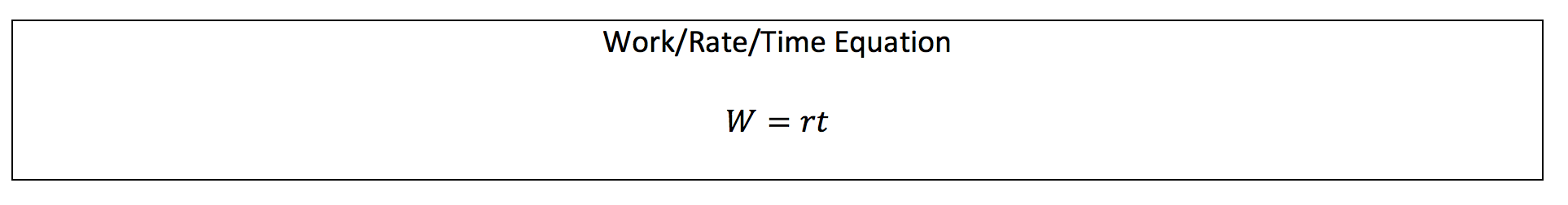
In this equation, W is the amount of work done/produced, r is the rate at which the work is completed, and t is the time in which the work is completed. In most cases, we will be able to determine two of these values and use algebra to solve for the third value. There is also an important point to make about the rate:

With these equations, let us look at a few examples.
Example 1: Multiple Workers Working at Different Rates
Rachel can build a house in 3 days, while Seth can build a house in 4 days. If Rachel and Seth work together, how long will it take for them to build 7 houses?
First, we need to calculate Rachel and Seth’s unit rates in houses per day.
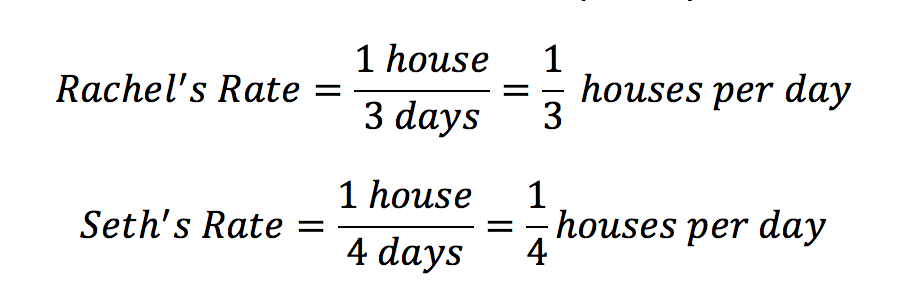
Once we have two units rates, we add them together to find a combined rates.
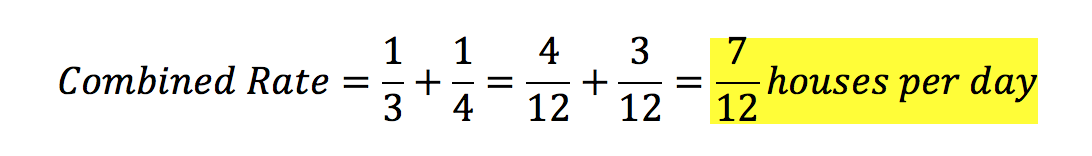
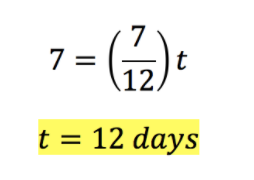
We solve algebraically for the missing value of t. It will take Seth and Rachel 12 days to build the seven houses. Now, let us move onto another version of this problem type.
Example 2: Multiple Workers Working at a Constant Rate
5 identical machines working at a constant rate can produce 12 widgets in 2 hours. How long will it take for 8 machines to produce 24 widgets?
For this problem, we will need a slight variation on our basic formula.

Here, the variable N will refer to the number of machines, whereas r still represents the rate of one machine. Let us use this formula with the given initial information, plugging in 12 widgets for W, 5 machines for N, and 2 hours for t. We will solve for the missing variable r.
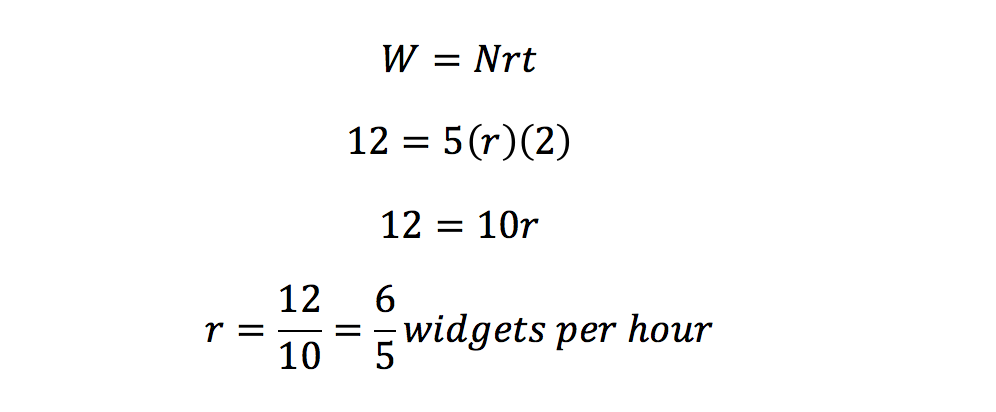
Now, we know the rate of one machine. What if 8 machines work together to make 24 widgets?
We use the W = Nrt equation again, this time plugging in 24 for W, 6/5 for r, 8 for N, and solving for t.
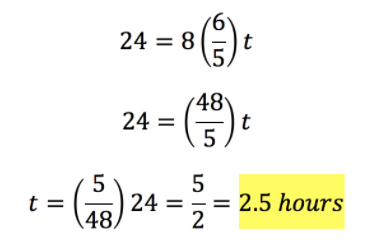
And we have an answer! It will take 2.5 hours for 8 machines to produce 24 widgets.
How does this approach apply to more difficult GMAT problems?
More difficult Work/Rate/Time problems apply the same principle but may require you to solve a system of equations and deal with more unknown values. To demonstrate, let us look at an actual GMAT problem:
Official Guide 2018: Problem Solving #113 from p. 162 of GMAT Official Guide 2018 (copyright 2017 by the Graduate Management Admission Council, published by John Wiley & Sons, Inc., Hoboken, NJ)
Three printing presses, R, S, and T working together at their respective constant rates, can do a certain printing job in 4 hours. S and T, working together at their respective constant rates, can do the same job in 5 hours. How many hours would it take R, working alone at its constant rate, to do the same job?
(A) 8
(B) 10
(C) 12
(D) 15
(E) 20
We begin with writing an algebraic representation of the first sentence “Three printing presses, R, S, and T working together at their respective constant rates, can do a certain printing job in 4 hours.” Our work W will be 1 job, our rate will be R + S + T, and our time t will be 4.
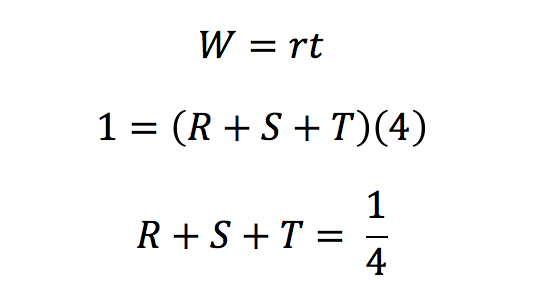
Now, we translate the second statement, “S and T, working together at their respective constant rates, can do the same job in 5 hours,” in the same way.
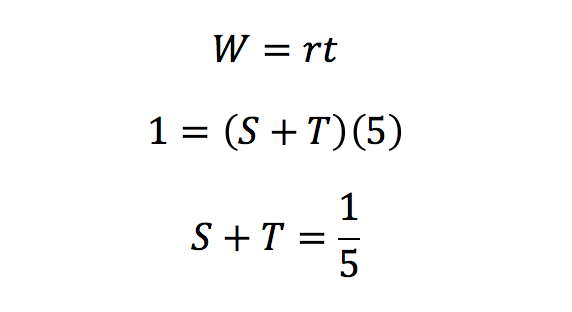
We are looking for how long it will take printing press R to complete the job by itself. We must find out the individual rate of printing press R. We can do this through substitution.
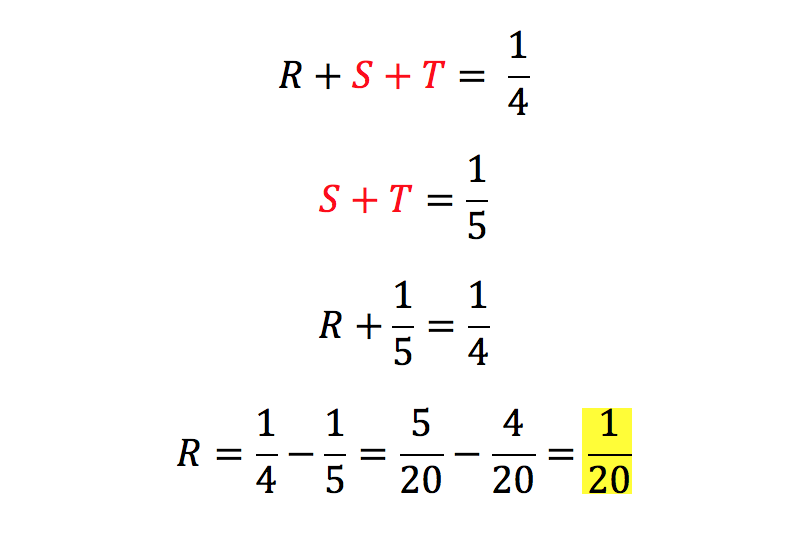
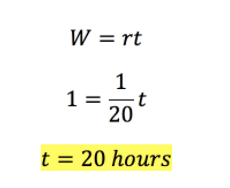
We have our answer! It will take (E) 20 hours for printing press R to complete 1 job.
In conclusion
There are a ton of concepts on the GMAT quant section, but certain problem types come up repeatedly. Work/Rate/Time problems comprise just one of these problem types, but if you learn how to tackle Work/Rate/Time problems, you can devote more energy to other questions on the exam. As always, be sure to keep track of any GMAT problems you miss during practice, and look for patterns in the question types you miss the most frequently – this is the best way to study and improve your score.
Comments