A brief introduction to the infinite

Set theory is the branch of mathematics that studies the infinite. The discipline was founded by  Georg Cantor in the late 1800s. Cantor is responsible for many of the notions we discuss here. A set, according to Cantor, is a collection of definite, distinguishable objects conceived as a  whole. A set consists of its elements. There is exactly one set with no elements and it is called the empty set. We refer to it thusly: ∅. We can define a set by either listing its elements or  uniquely describing them as a totality.  

The first important set we look at is N, the set of natural numbers.

It is often defined implicitly  via the following hint, so to speak: 

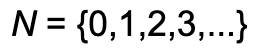
It is just a hint because it assumes that we somehow understand that these numbers increase  by one and go on forever. We can specify this set with a bit more precision. 

It can also be described more constructively as follows. Starting with a set N_0 = {0}, and for the largest element k ∈ N_n , let N_n+1 = Nn ∪ {k + 1}.

Finally, let the set:

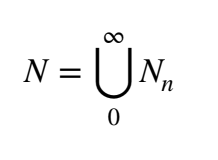
So N₁ = {0,1}, N₂ = {0,1,2}, etc.

All of the sets N₀,...,N_n are finite. Their union, the set N, is infinite.

In other words, we get our first infinite set by collecting all of the natural numbers into a single set. Another way to look at it is that N contains all possible sizes of finite sets. The notion of  size is a relatively obvious one for finite sets. The set S = {A, B, C, D} has the size 4. In set theory we call this size cardinality and we say that cardinality of S is 4 or || S || = 4. Cardinality of the empty set is 0. We will call the cardinality of the set N as follows:

A ⊂ B is read A is a subset of B. A ⊂ B if all elements of A are also elements of B.

Here are some interesting subsets of N: 

P = the set of all prime numbers 

O = the set of all odd numbers 

E = the set of all even numbers 

Z = the set of all integers {...,-3,-2,-1,0,1,2,3,...}

Here are two important supersets of N (i.e., N ⊂ Q ⊂ R): 

Q = the set of rational numbers (fractions of the form p/q where p is an integer and q is a  strictly positive integer) 

R = the set of real numbers. This set strictly extends Q.³⁴ 

It is clear that P ⊂ O ⊂ N ⊂ Z ⊂ Q ⊂ R.

Two sets have the same Cardinality if they contain the same number of elements.

For the finite  sets we establish this equivalence by  

1. well-ordering the set A. We choose the first, second, last element,
2. well-ordering the set B in the same way.
3. If one can order two sets using the same finite ordinal n, we say that the sets are of the || A || = || B || = n.

If two finite sets are equivalent in this sense, then we can pair their elements like this: 

• The first element of A with the first element of B,
• The second element of A with the second element of B,
• ...The last element of A with the last element of B.
  
  

This pairing enables us to generalize the notion of set size to infinite sets. Two sets A and B have the same cardinality if there is such a pairing of their respective elements. Each a ∈ A appears in exactly one such pair in the pairing. The same holds for b ∈ B.

If no such pairing exists, the sets are said to have different cardinalities.

If A is a subset of B but no such pairing exists, then B is said to be strictly larger than A, or || B || > || A ||.

Lemma 0.0.1.

Given a set A of finite cardinality n and an infinite set B, the cardinality of B is  strictly larger. 

Lemma 0.0.2.

|| O || = || E ||. 

In words, the set O of odd numbers is equinumerous to the set of even numbers E. The pairing is provided by the following map:

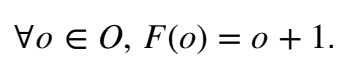
First note that ∃e ∈ E, o + 1 = e. It is easy to see that the map satisfies the uniqueness  requirements. This of course stands to reason; both sets are about half of infinity. It makes sense that they are about equal. Right?

The pairing looks like this, to be super obvious: (1, 2), (3, 4), (5,6), and so on.  

Lemma 0.0.3 (Or surprise 1).

The sets N and E have the same cardinality. There are exactly as many evens as there are  natural numbers. Think about this for a second. No wonder it was said that Cantor’s was the work of the devil. To prove the result, we define a map F satisfying ∀n ∈ N, F(n) = 2n.

To rigorously prove the lemma, we would need to demonstrate that the function F satisfies:

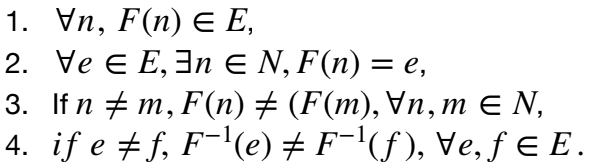
The intuition that we developed on finite quantities is starting to betray us here. We want to say  that the set of odd numbers is half as large as the set of all numbers, but the mapping proves  otherwise. It is advisable while hitchhiking in the infinite land, to take one’s intuitions with a  grain of salt.

Lemma 0.0.4.

||Z || = ||N ||

The sets Z of all integers and N of positive integers alone have the same cardinality. Map the negative numbers to odds, positive to evens as above. We are starting to get a sense that in the infinite arithmetic, infinity x 2 is not much different from the infinity x (1/2). 

Lemma 0.0.4.

||O|| = ||E || = ||P|| = ||N || = ||Z ||

Of course, we would need to prove that there are infinitely many primes. At this point one may  be tempted to give up on the notion of the infinite. As a reminder of the centrality of the infinite to mathematics, we briefly remind ourselves of the Euclidean proof of such result.  

One of the earliest results that convinced mathematicians that they may end up needing infinity  of some sort or another, was the proof that there are infinitely many primes. The proof  proceeded by contradiction asserting that there were no more than some finite number of primes and {p₁, p₂, …, p_n} was the complete list.  The proof proceeds to concoct a number P  called the Euclidean number that is defined as 1 + (p₁ × . . . × p_n) n. More formally, it looks like this:

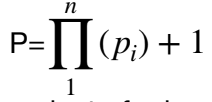
The first step into the abyss: ||Q|| = ||N||

The rational numbers and the reals seem very similar, at least on the surface. There seem to be  a lot of them, a whole bunch between any two rational numbers. Primes on the other hand seem to get rather rare as the numbers grow bigger. Because equivalence relationships are  transitive, if ||A|| = ||B|| and ||B||=||C||, then it follows that ||A||=||C||. Thus, if it turned out that  rational numbers are equinumerous with naturals, and primes with naturals, stunningly the rational numbers would be the same in number as the primes. The primes make up just above 0% of all natural numbers and natural numbers are essentially invisible among the rationals, and yet, the number of primes and rationals is the same. Rather shocking! 

Lemma 0.0.5 (Surprise 2).

||Q|| = ||N ||

The sets Q and N have the same cardinality. We will consider positive nonzero integers p, q in  p/q. We claim that once the map between this set and N is established, the extension to all of  Q is straightforward (using the methods outlined above in case of N and Z).  

We construct a matrix of all relevant p/q in Q as follows:

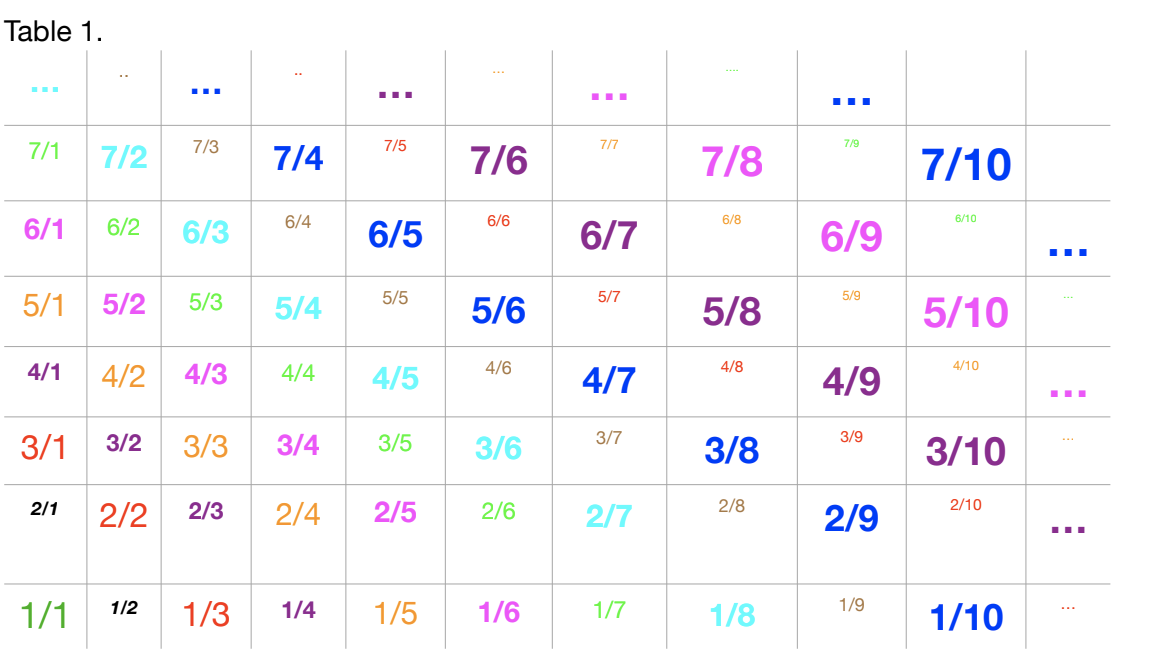
First, we note that for any given p, q ∈ N, p/q shows up somewhere in our matrix. As the numerator increases along the vertical and the denominator along  the horizontal axis, we follow p steps upwards, then on the line where each  fraction is of the form p/n starting with p/1, we count q steps to the right until we reach p/q.  

We define a function F that shows there are as many elements in Q as in N starting with 1/1,  F(1/1) = 1.

We notice that each finite k is k - 1 when we look at the size of the following set:

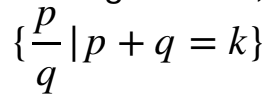
For k=2, there is one, 1/1, for k = 3,  there are two, 2/1 and 1/2. And so on. See Table 2.

We define the function as follows. For any k in N, we order the set as follows:

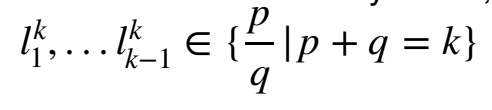
We then let

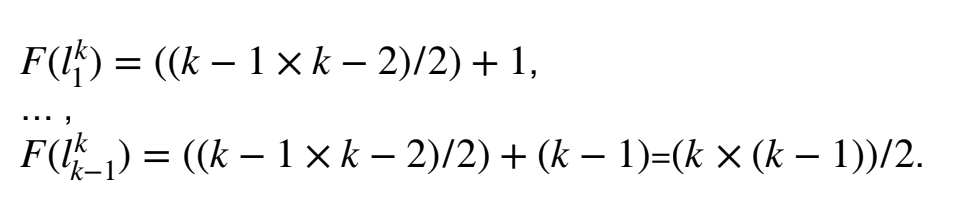
See Table 3 for illustration.  

The rigorous proof is needed but one can intuitively see that as the function F diagonally crosses the matrix in Table 1 in each pass, it eventually covers all pairs from Q with unique elements from N. So Q and N are shown to be  equinumerous as promised.  

These relatively easy equivalences raise an important question. Are their any infinite sets that are not simply equinumerous to the natural numbers? Is there more than one kind of infinite?

The second step into the abyss: ||N|| < ||R||

The set R is strictly bigger than N and hence than Q, Z, P, etc. via the  Diagonalization Argument. There is indeed more than one kind of infinite.  

Claim for contradiction: There is a function F : (R) → N that is one-to-one and onto. That means that we can form a countably infinite table that pairs reals and  naturals. For convenience we assume that the reals are from the interval [0,1] and that all tails are extended to infinity. For example, the real number 0.1 is turned into 0.09999999999999… We then have a sequence of reals between 0 and 1 mapped one-to-one onto natural numbers like so:

The diagonal is used to construct a real number m that could not have been caught by the function F, that is F(m) is undefined, contrary to the assumption that the mapping was one-to-one and onto. 

More on the kinds of infinities  

For set A, sets of all subsets of A, 2^A, and our transfinite series, we state the following without proof:

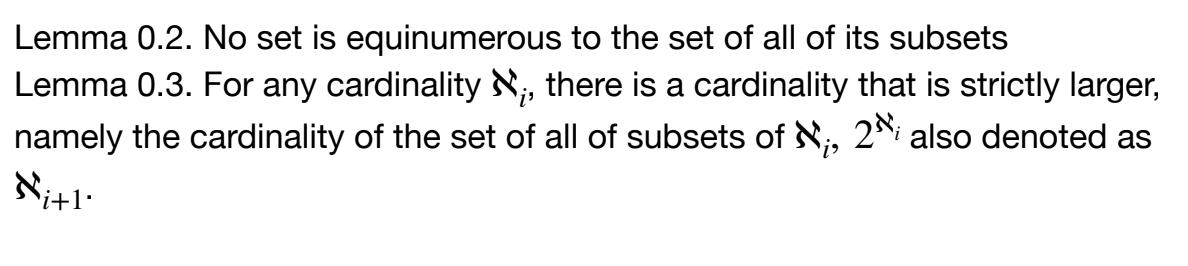
Theorem 0.1. There is infinitely many infinite cardinals 

Question: We showed using the diagonal argument that there are more elements in R than in N. We also showed that by taking the cardinality of the set of  subsets of natural numbers we can get a cardinal number strictly greater than  that of natural numbers. What we want to know is how much bigger is R than N? In particular, is ||R|| = ||2^N||?

As yet another surprise of the infinite realm, Cohen and Gödel have  demonstrated that the standard set theory in its present form does not rule out  either the claim of their equality not the opposite. The present day mathematics  is silent on the exact cardinality of the real numbers and the number sequence  as it extends into the transfinite. We know there is no largest infinite number, but the structure of their sequence still eludes us in a large part. We are only marginally closer to understanding the infinite than we were when Georg Cantor set out to do his seminal work on set theory. If god guided him in his  discoveries, as he claims, he left plenty of important discoveries in the shadows. They have remained so despite some of this tiny planet’s best minds ceaseless efforts. Perhaps god never seriously intended us to understand the infinite.  

Although Cantor was a devout Christian and he saw his work on the infinite as  inspired by his religion, others did not see it that way. The infinite being closely associated with the almighty himself, they claimed that Theorem 0.1. proved that Cantor was a polytheist of the worst kind. Not only did he think that there are  many gods, but he was committed, according to his critics, to there being an infinity of them, though as we saw they were not all equal.