Preparing for both mathematics sections on the SAT can be a bit intimidating. You can’t expect yourself to know every topic that might come up, and the time limit adds to the stress. Much more efficient than trying to learn everything you might come across is to start with what you have already learned in high school and use examples to apply it more widely in the SAT. The most classic sort of example is what teachers have been drilling for ages: plug in numbers. However, mathematics is all about generalizing rules and strategies, so I want to talk about how to expand plugging in numbers to the art of creating your own examples.
First, we are going to look at a normal example of plugging in numbers. An example SAT question might be[1]:
Now, if you are all brushed-up on your exponent rules, this problem is nice and algebraic and maybe even pretty. But if you are a bit rusty, we can get around the hard part of the problem. We just plug some numbers in for x or y to eliminate answers.
A few tips on plugging in:
- Pick easy numbers. 0 and 1 are much easier to work with than 7 or 12.
- Don’t over-plug--we want to remove variables, but leave the problem possible. For instance, in this question, we plug in a number for either or and find the other value algebraically. If we plug in for both, the expression breaks down.
- If unsure, plug in a second number.
Using these rules, we can plug in y = 0, so 3x = 12 or x = 4. Then the expression becomes 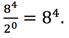 We can multiply this out by hand to find its actual value, 4096. This rules out B) and C), which multiply out to 256 and 64 respectively. A) also multiplies out to 4096, but we need to feel confident that D) isn’t right too. Since we aren’t sure, we follow rule 3 and plug in again. This time, we will do y = 3 (we pick a value of y so that x is a whole number, following rule 1). Then we get:
We can multiply this out by hand to find its actual value, 4096. This rules out B) and C), which multiply out to 256 and 64 respectively. A) also multiplies out to 4096, but we need to feel confident that D) isn’t right too. Since we aren’t sure, we follow rule 3 and plug in again. This time, we will do y = 3 (we pick a value of y so that x is a whole number, following rule 1). Then we get: 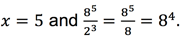
This is the same thing we got last time, which makes us much more confident on A) as the right answer.
It’s worth noting that we are not entirely certain through this method; these values might have been coincidences, but it seems unlikely at this point and a confident guess is much better than leaving the question blank. We don’t want to spend too much time on an individual question, though, so we are going to leave it at that.
Using Examples
Now, we are going to expand on that method. No longer do we just plug in numbers, we plug in whole examples instead! The sample problem here is question 29 from the calculator section of the same practice test.
Almost every student to whom I have shown this problem has been a bit confused, and for good reason! This question examines topics that are not frequently covered in a math curriculum—synthetic division and the properties of polynomials. However, we can make a few example polynomials that p(x) might clarify the problem. For example, p(x) = x- 5 satisfies the condition (i.e. p(3) = 3 - 5 = -2) and rules out B) and C). But we still don’t know if A) or D) is valid, so by rule 3, we try another example. We might pick p(x) = 2x - 8 = 2(x - 4). This example shows that none of the listed linear terms are factors of p(x) so D) is the right answer. Even though we might not even know what the answer is saying, we were able to rule out all of the other possible answers that we did understand.
Going Beyond the Exam
Anything I teach in preparation for a standardized exam I try to make applicable outside of the exam. Using examples like these will serve you for generally learning mathematics. To flesh out a concept that you have recently learned, it can be helpful to pick out and test unusual examples. For instance, a topic that frequently comes up with students soon after the SAT is “limits”. These tools consider the continuous properties of functions. Instead of looking at the value of a function at a point (i.e. f(2) = 5), we look at the value the function tends to at a point, which we write:
Frequently these two italicized phrases line up. An example might be f(x) = 2x . When we plug in 2, we get f(2) = 2 * 2 = 4. The function is a line, so as we plug in points closer and closer to 2, we get values closer and closer to 4:
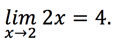 Now we can use another example to understand when the two italicized quantities are different to get a full sense of the properties of limits. We will create an excessively didactic example: a function, g, that is equal to 1 everywhere except for when x = 0, where g(0) = 0. If we plug points into that are closer and closer to 0 (but not 0), we keep getting 1. So the value the function tends to at 0 is 1:
Now we can use another example to understand when the two italicized quantities are different to get a full sense of the properties of limits. We will create an excessively didactic example: a function, g, that is equal to 1 everywhere except for when x = 0, where g(0) = 0. If we plug points into that are closer and closer to 0 (but not 0), we keep getting 1. So the value the function tends to at 0 is 1:
which is different from the value we get when we plug in zero itself! We illustrated the properties of limits simply by taking examples.
And you can do this at home. Whenever you are struggling to understand a concept, try to make some examples to examine it. This is an art, and it isn’t always obvious what examples to pick. But skill and practice that you build up will have applications across all of the math you study (and the SAT!).
Are you interested in getting set up with an SAT mathematics tutor?
[1] (this sample problem is question 14 on the no-calculator section of the sample test available here)
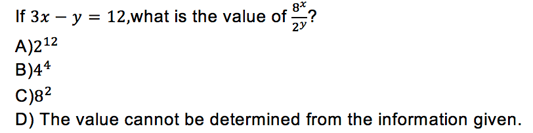
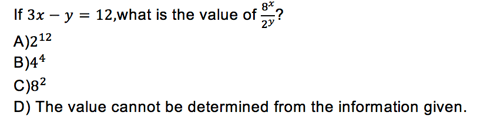
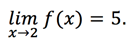
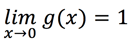

Comments