An introduction to potential energy

Potential energy can be easy to understand, tricky to define, and confusing to use. Here, we not only define potential energy, but explain what it means, why physicists use it, how physicists calculate it, and examine why potential energy is only associated with certain types of forces.

Why do we need potential energy?

Here’s one definition that pops up if you Google potential energy: “Potential energy is the energy that an object possesses due to its position or configuration in a system.” I don’t know about you, but that definition is not helpful at all for understanding what potential energy actually is.

So let’s try another way. Imagine a simple setup. You stand on the ground, and you throw a ball upward.

To explain its behavior in terms of kinetic energy, we might say: when the ball is thrown, it possesses some kinetic energy. As the ball continues upward, its kinetic energy decreases, hitting zero when the ball reaches its apex, and increasing again on its way down.

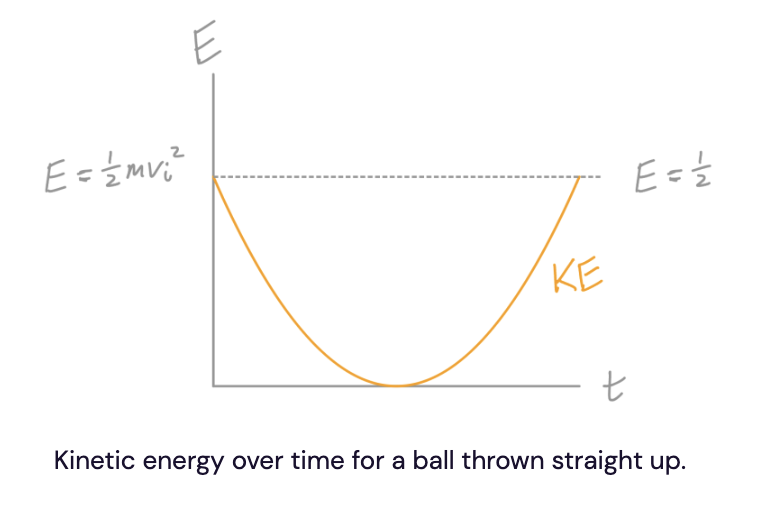
How is it that ball can start with some kinetic energy, but this energy disappears when it reaches the apex? Where did the kinetic energy go?

Well, why does it have to go anywhere? Why can’t it just disappear? None of the basic kinematic laws require us to incorporate kinetic energy. If we have a ball thrown upward and we know its initial velocity, we can describe and even predict its motion without ever talking about kinetic energy, potential energy, or any other type of energy. So far, there’s nothing impermissible or inconsistent about saying the kinetic energy first disappears when it reaches the apex, then reappears on the way down.

However, this explanation probably feels icky to you because it violates the seemingly obvious principle of conservation of energy. Energy can’t just magically disappear or appear, right?

Enter potential energy. Physicists define a quantity called potential energy that represents the amount of energy “stored” in the object. Now, we can say that the kinetic energy didn’t just disappear – it was converted into potential energy as the ball travels up, and converted back into kinetic energy energy on the way down.

In principle, we could describe our universe without invoking potential energy or energy conservation. However, while we might still gleam some physical insight, our theories would be found wanting. Incorporating potential energy can not only make the calculations easier, but also opens up additional insights and predictions.

But what if we didn’t know how the ball got to the apex, yet still wanted to know what happens to it next? What if we wanted to know how fast it’s moving on the way down? Potential energy can help us find these answers.

By introducing potential energy as a “bookkeeping device” to ensure energy is conserved, we can describe, model, and predict physical phenomena in terms of energy, opening up new calculations and insights.

Defining potential energy

Let’s revisit the Google definition, specifically the part that defines potential energy as the energy “that an object possesses due to its position or configuration in a system”. An object possesses potential energy because it’s part of a force field.

Another way of thinking about it: there needs to be some force field that “captures” the kinetic energy; otherwise, the object would just keep on moving with an unchanged kinetic energy.

In our previous example, the ball possesses potential energy because it’s part of Earth’s gravitational system. As the ball travels upward against the gravitational force, the gravitational field “captures” some of the ball’s kinetic energy, converting it into gravitational potential energy.

Physicists quantify this transfer of energy by introducing a quantity called work.

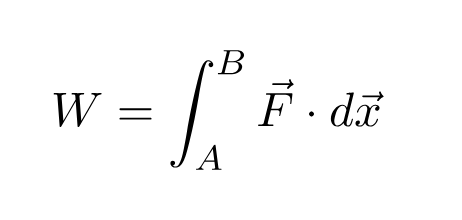
See here for a deeper dive into the work definition and its full implications, but what’s important to us is that work represents the amount of energy needed for a force F to move an object from point A to point B. Combining that fact with conservation of energy leads us to this relation:

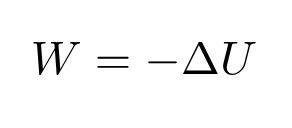
This equation states that the change in the potential energy of an object is defined as the negative of the work performed on the object.

• If work is negative, potential energy increases.
  • Work is being done on the object against the force direction (to see this, note that the dot product will be negative if they’re in different directions)
  • In our ball example, the object is moving deeper into the gravitational force field, converting kinetic energy into potential energy.
• If work is positive, potential energy decreases.
  • Work is being done on the object along the force direction (the dot product will be positive if they’re in the same direction)

Potential energy requires conservative forces

Gravitational potential energy is not the only type of potential energy. Other types include:

• elastic potential energy – features a restoring force from a spring not at equilibrium
• nuclear potential energy – features the strong and weak nuclear force acting on
  
  

In fact, any conservative force will have a potential energy associated with it. In fact, it’s called a conservative force because energy is conserved when this kind of force acts on an object.

There are a few different ways of defining a conservative force, all of which are equally valid, as they all imply each other.

1. When a conservative force acts on an object, the force’s direction and strength depends only the object’s location.
2. For an object acted upon by a conservative force, the work to move an object from Point A to Point B is path-independent. The potential energy depends only on the location of the object, not the path taken to get there.
   
   

If a force is not conservative and any of these criteria aren’t satisfied, then potential energy isn’t well-defined.

• As we’ve defined above, the change in potential energy is equal to the work needed to move the object. If the work depends on the path taken, then the change in potential energy from Point A to Point B can taken on different values depending on the path.
• However, the definition of potential energy is energy that an object possesses due to its location in the system. It must always have the same value at Point B, regardless of how it got there.
  
  

Gravity is a conservative force, a fact we’ve relied on throughout this post. So is the restoring force from a spring. Friction is an example of a non-conservative force: it depends on the normal force and does not depend on the object’s location (one reason that we don’t intuitively think of friction as “storing” any energy).

Want to learn more from Max? Check out his other breakdowns from his personal blog here.