What is a Fermi approximation?
The only thing that physicists like more than dimensional analysis is a good order of magnitude estimation, also known as a Fermi problem or Fermi approximation. A classic is the piano tuner problem: “How many piano tuners are in the city of Chicago?”
If you were to just guess a number in response, there’s a pretty good chance that you’ll be way off. You probably know there aren’t 1 million or only 10 piano tuners in the city, but it’s hard to know if 100, 1,000, or 10,000 tuners feels most correct. How do we tackle this problem? The basic principle behind answering this question and others like it is to guess factors of the answer, rather than immediately guess the answer itself.
“Factoring” your answer
The crux of guessing factors related to your answer is to involve many different points of approximation in order to have your underestimations and overestimations cancel out. As an example, let’s consider a more relatable question: “How much does a typical Starbucks make in one year?”
We could think of the answer as a product in the following way:
- The amount of money a Starbucks makes in a year is the amount it makes per day, times 365, if we assume every day is about the same.
- The amount of money a Starbucks makes in a day is about the amount it makes per hour, times the number of open hours.
- The amount made per hour is about equal to the number of transactions in that hour times the amount per transaction.
We could summarize the above as:
(Money per year) = 365 (number of open hours) (transactions per hour) (money per transaction)
We’ve successfully taken our problem from estimating something which is hard to wrap our minds around (the amount of money in a whole year) to something most of us can probably imagine (the amount of money per Starbucks transaction and the frequency of transactions).
Let’s put some numbers in!
- A typical Starbucks transaction for each customer is probably around 5 dollars. Some people buy only drinks (probably less than 5), some get a drink and a snack (probably more than 5), so it averages out.
- Let's say Starbucks processes an order every 2 minutes (based on the wait times I've seen). That comes out to 30 orders an hour. Usually, coffee shops are open for about 12 hours a day, from early morning to afternoon. As such, Starbucks processes about 360 orders a day.
- It might be a stretch, but let’s say that Starbucks is open every day, so we'd get about 131,400 orders a year. With each order priced at 5 dollars, that comes out to 657,000 dollars in revenue!
The actual annual revenue of a Starbucks is averaged at 808,000 dollars, so our approximation isn’t too bad at all!
Why does this work?
Let’s try to understand this point earlier about our overestimations and underestimations cancelling out. How exactly does that work?
If we call our factors a and our answer X, then our answer takes the form:
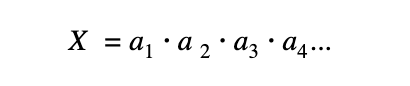
It’s likely that we tend to overestimate certain factors, such as the number of transactions per hour, and underestimate others, such as the price per transaction. Perhaps we are a factor of 3 too large on one and a factor of 3 too small on the other. The final answer has no extra factors at all because 3 and ⅓ would cancel out!
The magic of Fermi approximations lies in this concept, making this simple technique extremely powerful for getting order of magnitude estimations. You can now answer questions like “How many pieces of paper could a package of pencil lead cover?” or “How many new cars does a dealership sell per month, on average?”
Physics – from high school physics to physics at the graduate level – can be quite challenging. That's why we maintain a staff of physics PhDs and working professionals who are committed to the art of teaching. There is no course or standardized test that we do not have extensive experience teaching. Want to learn more?


Comments