Math is relevant to every day life, though it is certainly a language that requires patience to learn and practice to upkeep. While most of my work these days uses a very different kind of math – mostly statistics and regression – my love of baking helps me keep up some of my fundamental algebra skills.
In this blog post, I’ll teach you some of the basic concepts in baking a loaf of bread and demonstrate the ways that fundamental math skills are invaluable for both the process and the product!
1. A bit about bread
The four main ingredients of bread are flour, salt, water, and yeast. In many types of flour there are proteins called gliadin and glutenin. When mixed with water, these two proteins form a mesh structure known as gluten. Salt, in small amounts, helps make the network of gluten into a more well aligned and even mesh.
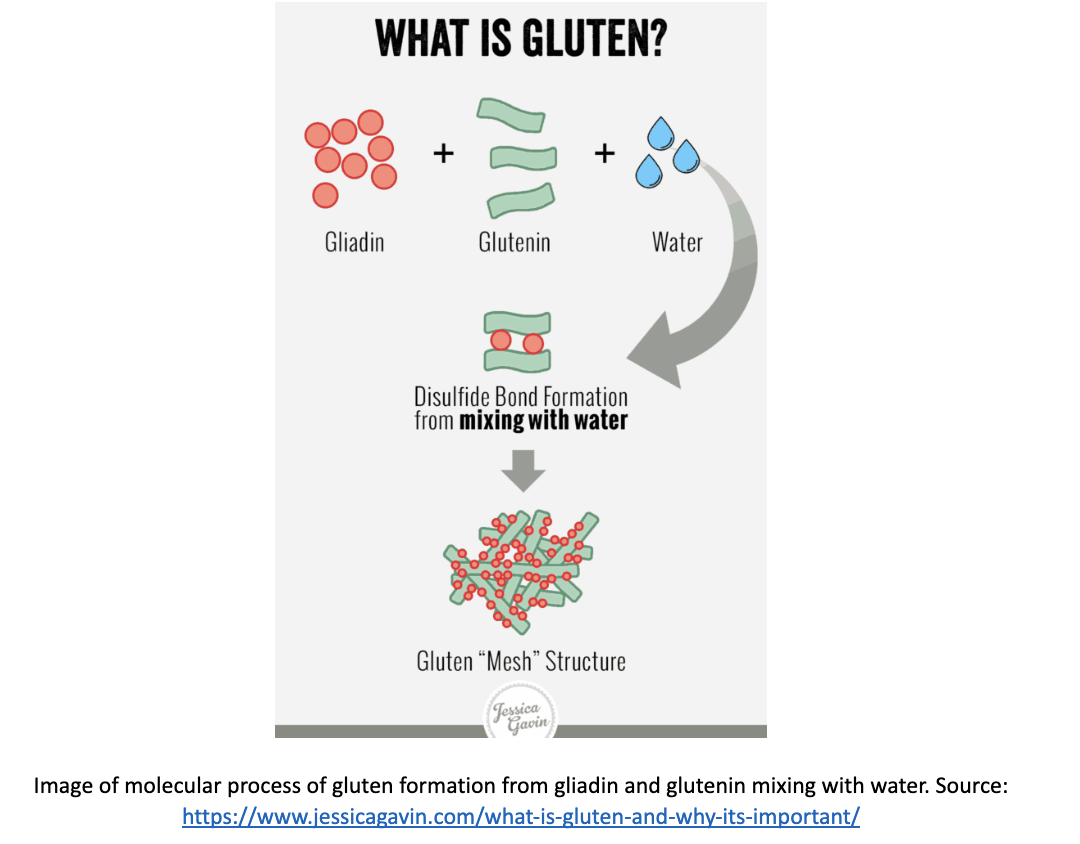
Enzymes help break down complex sugars (i.e. starches) in the flour. The yeast then consume the simple sugar molecules and produce carbon dioxide, which inflates the little pockets of space inside the gluten mesh. This inflation is what helps the bread become fluffy and delicious, rather than a solid mass of nearly inedible dough!
2. Baker's percentages
One of the fundamental mathematical tools for bread baking is the use “baker’s percentages.” The idea is that the quantity of flour becomes the baseline from which every other ingredient is compared and the amount of dough you make can be scaled up or down based on the baker’s percentage formula (in most cases).
Let’s look at a quick example of a standard dough formula for making a single loaf of bread and compare total percentage to baker’s percentage:
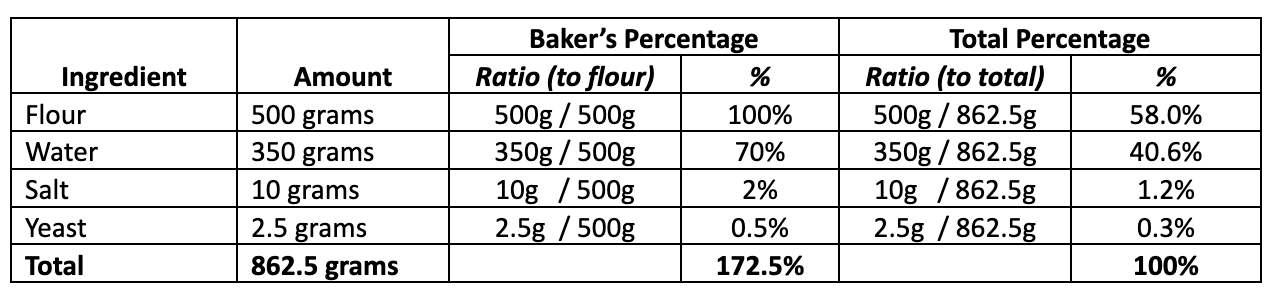
The utility of the baker’s percentages comes from the fact that the different ingredients are more directly related to one another than to the overall combination of all ingredients.
This is a helpful way to manipulate one of the most important ratios in all of baking: water to flour. Many artisan bread doughs rely on a ratio of 65-80 parts water to 100 parts flour, or 65-80% (flour) “hydration” (by mass), where the percentage tends to be higher for doughs with more whole wheat flour because it absorbs more moisture per gram of flour.
3. Manipulating baker’s percentages – Example 1
Now let’s say that I have some friends coming over this weekend and want to make a slightly larger loaf. I know from experience that making a loaf with 600g of flour still fits within my proofing basket, but is large enough to help feed a few more people.
Applying the baker’s percentages to calculate the quantities of all ingredients:
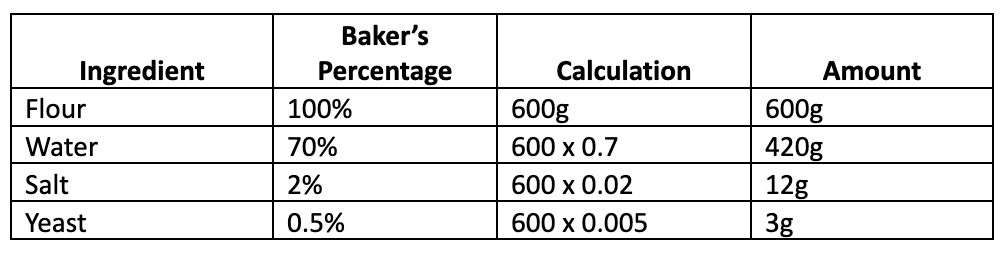
Now, I mentioned earlier in this post about people having trouble with tips at restaurants. At first, some of these calculations look like they might require a calculator or some complicated division. However, by making use of easier to do calculations, here is how I can more easily and quickly arrive at these final numbers in my head:
Water: 600g x 0.7
Using the cumulative property, I can divide up this calculation into more familiar pieces that I rearrange to make individual calculations easier to do in my head:
(6 x 100) x (7 x 0.1) = 6 x 100 x 7 x 0.1 = 6 x 7 x 100 x 0.1 = 42 x 10 = 420g
Salt: 600g x 0.02
For this calculation, I know that 1% of 600 is easier to think about, so I calculate that as: 600 x 0.01 = 6g
Then, I know that what I need is double that (2% rather than 1% of 600): 6g x 2 = 12g
Yeast: 600g x 0.005
Again, I initially think about this in relation to 1% of 600g = 6g
Now I need ½ of 1% so 6g / 2 = 3g
4. Manipulating baker’s percentages – Example 2
And for another example…let’s say that I have some extra free time this weekend and want to get some practice making a batch of four loaves at a time – from which one will undoubtedly be eaten the day it is baked, another will be eaten over the course of the next few days, and two will either be sliced and frozen (best way to store the bread for a while!) or my partner will force us to give the bread away to friends and coworkers.
However, for these loaves I want to make them with some whole-wheat flour included, so we will separate the total flour into two parts and also increase the hydration percentage slightly.
Let’s apply the baker’s percentage method to help calculate the total amount of ingredients I will need to add to create the dough. To start, I know that four loaves will need 500g x 4 = 2000g of total flour.
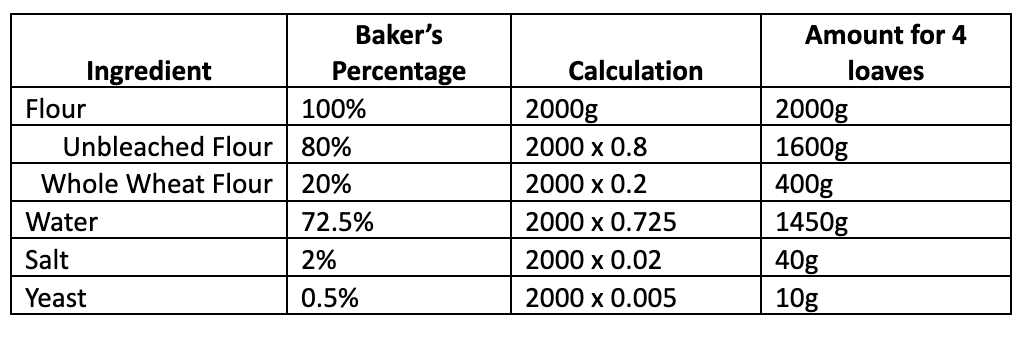
Similar to the calculations for Example 1, here I do the following calculations:
Unbleached Flour: 2000 x 0.8
I know that 80% of 1000g is 800g, so now I can easily do 800g x 2 = 1600g
Whole Wheat Flour: 2000g x 0.2
Here, I could do a similar approach as with unbleached flour, but the other easy option is using the cumulative property and decimal movements (with multipliers of 10) to find that:
2 x 0.2 = 0.4 and 0.4 x 1000 = 400g
Water: 2000g x 0.725
First, I determine that 0.725 of 1000g = 725g by moving decimals three places.
Then, I can manage 725g x 2 by calculating that 700 x 2 = 1400 and 25 x 2 = 50.
So 1400 + 50 = 1450g
Yeast: 2000g x 0.005
Finally, 2000g x 0.01 = 20g, so 20g / 2 = 10g


Comments