
Hi, again! I’m back with more useful tips for demystifying physics. In my first post, I discussed how staying abstract and saving the calculator for the end of the problem helps us to work through the math of a physics problem more quickly and confidently. In the next two posts, I’m going to describe a clever technique that allows us to skip the math altogether in certain types of problems! Keeping this trick in mind will help you when tackling your high school or college problem sets and will make you much more efficient when studying for the SAT 2 or physics GRE.
Find the numbers that matter, then arrange them to get what you want
The key here is dimensional analysis. This technique is all about physical intuition. Any physical system is defined by some set of numbers: the length and stiffness of a spring, and the mass of the block attached to the spring; the area and separation of two plates of a capacitor, and the dielectric constant of the material in between. It makes sense, then, that the answer to any question about such a system has to depend on some of these numbers in a sensible way. Sweeping the math under the rug for the moment, we only need to figure out how to mix and match these numbers in such a way that the result has the same units as the answer we’re trying to find. If there is only one way we can arrange those numbers, then the result we get should be pretty close to the actual answer.
Let’s take a simple example. Say we’re sitting in the test center and we’re struck by amnesia; we can’t remember the formula for the oscillation frequency of a pendulum! We know there’s a square root (or maybe a squared?) in there, and something about g, or maybe k, but we can’t quite remember how the formula goes.
Well, what are the physically significant numbers here? The pendulum has some length l, which is probably important. It makes sense that a longer pendulum might swing more quickly or slowly. Gravity is the force that makes the pendulum swing, so let’s put g on the list. The block at the end of the pendulum has a mass m, so let’s put that on the list, too. That seems to be it; making the usual nice assumptions about massless strings and no air resistance, nothing else really matters for the problem.
So we’ve quickly jotted down the following notes, where [x] means “units of x”:
[g] = m/s2
[l] = m
[m] = kg
We’re trying to find the frequency of the pendulum’s swinging, so we’re looking for an answer with the units of hertz, or seconds-1. We can see that the only seconds we have to work with are in g, so that needs to go into our answer. We still have the pesky meters in the units of g, so we can cancel that out by dividing by l. We now have [g/l] = 1/s2, so we just need to put this expression under a square root to find
![]()
with
![]()
This is the exact answer we’ve been looking for! Keep in mind, though, that as in many instances in physics, we are dealing with the angular frequency, so the period of the pendulum's oscillation is given by
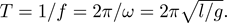
You might notice that we’ve left out the mass of the block at the end of the pendulum, and for good reason. In terms of units, there are no other units of mass that need to be cancelled. Physically, when we increase the mass of the block, two things happen: gravity exerts a larger force on the pendulum (Fg = mg) and a larger force is needed to accelerate the pendulum (F = ma), so m cancels out.
What we can learn, what we can miss
This technique comes with a big caveat, though. Dimensional analysis completely misses numerical factors! Should there be a factor of pi? 2 pi? ½? Should it be sine or cosine? We don’t know, and units won’t tell us.
So if we need a numerical answer, use dimensional analysis with care. Consider the reverse process, using units to check our answers. Say we’ve just done the math to find the final velocity of a drag racer at the end of a track. Checking our units will tell us that we need to go back through our math if we come up with an answer of 23 kg m2/s. The check won’t tell us that an answer of 15 m/s is necessarily correct, however. There still might be a simple math answer (add instead of subtract, dropped a factor of ½, etc.) lurking in our solution to the problem.
In the same way, it’s difficult to use dimensional analysis alone to arrive at a numerical answer with a high degree of confidence. Then where should we use this technique? In our next post, we’ll explore a few ways in which this technique can be tremendously useful on test day or when tackling a problem set. Stay tuned!
Comments