Every physics experiment involves error. Let me show you how to understand, embrace, and communicate your uncertainty.
In previous posts, we’ve focused on the theoretical side of learning physics, going over various techniques that will enable you to tackle problems, whether on the physics SAT 2, the physics GRE, or in your high school and college physics course, with confidence and ease. In the next two posts, let’s focus more on the experimental side of learning physics.
Whenever you perform an experiment and write up the results, whether you’re timing the swing of a pendulum in your first high school physics class or submitting your fifth paper to Nature, you need to account for errors in your measurement. No measurement is perfect; every measurement you make will have some finite uncertainty associated with it, and you need to make sure that your final result accurately reflects the inevitable imperfection of your measurement.
Our experiment: measuring gravity
For example, imagine that we are asked to find g, the acceleration due to gravity, by dropping a ball from a given height. What are the two measurements that we need to make? We need to measure the time t the ball takes to hit the ground and the height h from which we dropped it. We can then find g using the formula
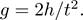
This is a very simple experiment – all it takes is a ball and a stopwatch – and the errors we consider are specific to the measurement at hand, but it illustrates several concepts that apply to any experiment you might want to perform.
Measuring time: accuracy versus precision
First, let’s look at our measurement of t and ask ourselves both how precise and how accurate it is (and these are two different questions). The precision of a measurement reflects how specific the number you measured is. In our example, that corresponds to the number of digits in our stopwatch's display. Say we read off all the digits the stopwatch has, giving us 0.62 s. The precision of this single measurement is then 0.01 s.
How accurate is this measurement, though? That is, how sure are we that 0.62 s is the actual time it took for the ball to hit the floor? The accuracy of a measurement reflects how well the value you measured matches the actual quantity you are trying to measure. The average human reaction time is around 200 ms, so it doesn’t make sense to claim that we can make a measurement by eye that is accurate to 10 ms, which is our precision. We’re simply not fast enough with our trigger fingers.
What uncertainty do we claim?
Now that we understand the precision of our time measurement (0.01 s) and we have some idea about the errors that are present in our experiment (our human reaction time), what uncertainty in our measurement can we responsibly claim? This is the part that takes some judgment, and we should remember that the purpose of quoting an error in our measurement is to indicate how sure we are of our answer. We should be guided, then, by the thought that it is better to admit when you are uncertain about a result than it is to claim a result with certainty but be wrong.
But what do we write down? First, let’s notice that our human reaction time (200 ms) is much longer than the precision of the stopwatch (10 ms), so we can ignore the uncertainty due to the precision of our measurement and focus on the accuracy. That is, our trigger finger, and not the stopwatch, is the limiting factor in the experiment.
So what can we claim? Let’s start with the easiest, most conservative estimate, then ask ourselves if we can make any assumptions. The average reaction time for pushing the stopwatch button is 200 ms, so let’s say that, on any given push, we can be anywhere from 0 to 400 ms late. Then both the start time and the stop time have an uncertainty of ±0.2 s. Since we add the absolute uncertainties of quantities that are being added or subtracted, the fall time t, defined as
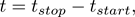
has an uncertainty of.
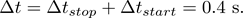
Thus, the measured time that we can quote is 0.6 ± 0.4 s.
Notice that we read 0.62 s from the stopwatch, but dropped the second sig fig from 0.62 and only claim 0.6 ± 0.4 s. I’ll say more about this when we discuss how we present our final result, but if our uncertainty is so much larger than our precision, then it doesn’t make sense to give such a precise number. Imagine trying to describe a person you just met; would it make sense to claim that she was 5 feet, 4.175 inches tall, give or take 2 inches?
Can we do better?
This is a huge uncertainty, though! We are saying that the ball’s fall time can be as little as 0.2 s or as much as 1.0 s, a difference of a factor of 5! Can we responsibly claim a smaller uncertainty? Here’s where we should think more carefully about what actually goes on during the experiment. We might notice that the average human reaction time is around 200 ms, but the statistics are more detailed than that.
If we assume that we are purely reacting to the sight of the ball starting to fall or hitting the ground, then we could assume that our reaction time follows the statistical distribution for the general population. We can then reasonably claim that, with high probability, we were somewhere between 150 ms and 350 ms late on both button pushes. Both the start time and the stop time are late by an average of 0.25 s, which cancels out, with an uncertainty of 0.1 s. With this assumption, we can then quote a measured time of 0.6 ± 0.2 s, a much more precise result.
When possible, don’t assume – measure!
If all of these assumptions and justifications make you uncomfortable, perhaps they should. When you give a result, any claim you make is only as valid as your justifications for doing so and the assumptions that you make. What if our assumption that we are purely reacting to the ball hitting the ground was wrong? What if we followed the path of the falling ball and tried to anticipate when it would hit?
We also might have missed other sources of error. What if there are things that our reasoning missed? How soon exactly after our partner lets go of the ball can we tell that it is actually falling? If we were the one who said “go,” did our partner drop the ball 200 ms after we started timing, instead of the other way around? Often, it is very difficult to predict every source of error that could throw our measurement off, some of which are quite subtle.
When possible, we should try to measure our uncertainty instead of making guesses, assumptions, and justifications. In the next post, let’s explore how we can measure this uncertainty and come to a more precise and more accurate result.
Comments