
In this series of posts, we’ve been exploring some of the handy physical intuition and convenient symmetries that can help demystify your electricity and magnetism course. Whether taking your first high school physics course, a college E+M course, or the physics SAT II, the introductory equations of E+M can be difficult to keep straight.
We began in the last post by looking at the physical intuition behind Coulomb’s law, one of the most important early equations you will meet. You can think of a point charge as emanating an electric field, much like the sun emanates light. If the total quantity emitted, called the flux, of electric field is given by Q/ε0 and the flux is spread evenly in all directions over a sphere of surface area 4πr2, then we can see that the intensity (= flux/area) of the electric field at any point on the sphere is given by Coulomb’s law:
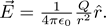
Reason by analogy to extend your knowledge
One of the most powerful techniques you can learn while studying E+M, and physics more generally, is learning and reasoning by analogy. We will say more about this technique in later posts, but the concept is that if the math describing two different objects looks the same, there is a good chance that the superficial similarity hints at a deeper connection. For example, compare the electrostatic attraction from Coulomb’s law,
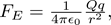
to the expression for gravitational attraction,
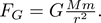
Putting quantum mechanics aside for a moment, is it any surprise that an electron orbits the positively charged nucleus much like our planet orbits the sun? This, in fact, was the dominant picture of the atom for a short span early in the 20th century.
Biot-Savart – a magnetic analogy to Coulomb’s law
Can we find such an analogy that extends our intuition for electric fields to magnetic fields? Yes, we can! The analog to Coulomb’s law for magnetism is the Biot-Savart law:
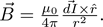
The analogy is clear, and very convenient. Electric fields are created by charges, and magnetic fields are created by currents, or charges in motion. Therefore, instead of some point charge Q, we have some infinitesimal bit of current dI. This dI just represents a current I being carried along an infinitesimally short wire in some direction. The physical constants also change, but you only need to remember that ε0 corresponds to electric fields and belongs in the denominator, while μ0 corresponds to magnetic fields and belongs in the numerator.
The other significant difference is the inclusion of the cross-product, dI x r, in the numerator. For the electric field, the point charge Q is simply that, a point. Logically, we know that the field created by one point can only point directly toward or away from that point (what other direction could it have?), so the direction of the electric field is easily defined to be radial. For the magnetic field, though, the current dI itself has a direction; it is not simply a point-like object. The direction of the magnetic field at a given point is therefore defined by both the direction from that point to the current (r) and the direction of the current itself (dI). The cross-product just states that the B-field vector is perpendicular to both r and dI, but you should usually skip the vector algebra and use the right-hand rule to find the B-field’s direction.
That’s it! That’s how you can easily adapt from using Coulomb’s law to work with collections of charges to using the Biot-Savart law to work with collections of currents.
Analogy is useful, but know when its usefulness ends
As with any analogy, you need to be aware of where the usefulness of the Coulomb-Biot-Savart analogy ends. You might be tempted to imagine an analog of Gauss’s law for magnetic fields. You might imagine that a current dI creates some flux μ0dI that is then spread over a sphere’s 4πr2 surface area, but this picture is incorrect. There is, in fact, an analog of Gauss’s law for magnetic fields, and it states that the magnetic field flux passing through a sphere, or any closed surface, is zero, regardless of any currents.
We can understand this by looking at the directions of the electric and magnetic fields. Electric fields emanate out from charges, but magnetic fields wrap around currents. If all magnetic field lines form a closed loop, then any closed surface you can draw will have equal numbers of magnetic field lines entering and leaving it, resulting in zero net flux.
Learn the analogy, and use it!
Still, the close analogy between electric and magnetic fields can be extremely useful. In the next lecture, we’ll explore some specific instances in which the close parallel between Coulomb’s law and the Biot-Savart law can be very useful. Stay tuned!
Comments