But what is “dx” really? Calculus terms explained

The symbol “dx” comes up everywhere in calculus. For example:

• If y is a function of x, then we sometimes write the derivative of y with respect to x as the following:

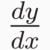
• When we write indefinite integrals, they are written as:

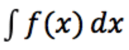
• When we write definite integrals, they are written as:
  

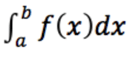
But what is “dx” really? It’s more than just notation! In this post, we’ll explore the meaning of “dx” and try to get a better understanding of some of the symbols that we often see in calculus.

Calculus as the study of infinitesimal change

Calculus is the study of continuous change, or infinitesimal change. To get an idea of what this means, let’s consider the following: suppose that you’re running a race. You begin running at time x=0 seconds and then track your displacement as a function f(x). Your displacement function f(x) is then a continuous function that varies over time.

Suppose now that you wanted to know your speed at time x=10 seconds. That is a calculus question since you are looking for a rate of change at one particular time. How could you do this? Well, you might estimate your speed at time t=10 as our average speed between time x=10 and x=11, which can be expressed as:

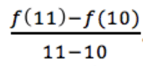
But you could get a better estimate by choosing a smaller time interval, say from x=10 to x=10.1 instead, or even better from x=10 to x=10.01.

Really, what you want to do is to take the limit as the size of your time interval goes to zero. That is, you want to take an infinitesimally small change in x. Then, by the definition of a derivative, your speed at x=10 seconds is:

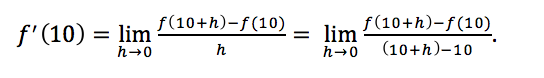
We should think of h going to zero as taking smaller and smaller increases in x when we take the average speed from time x=10 to time x=10+h.

This is where “dx” comes in.

"dx" is an infinitesimal change in x. We can think of "dx" (read as dee-ex) as an infinitesimally small change in x. The "d" in "dx" should remind you of a delta ∆, which is the symbol for change. "dx has no numerical value. Rather, it captures this idea that occurs a lot in calculus of taking the limit of smaller and smaller interval sizes to figure out something precisely about a continuous function.

We can see this if we revisit our speed example from earlier. When computing our derivative

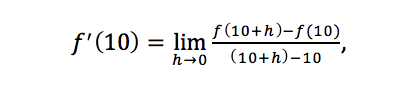
The bottom of this fraction is (10+h)-10 as h goes to zero, which is an infinitesimally small change in x. We might therefore think of the denominator as h goes to zero as dx. If we let y=f(x), then the numerator of this fraction is f(10+h)-f(10) as h goes to zero, which is an infinitesimally small change in y, or dy. Putting this all together, we recover the notation:

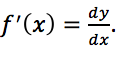
That is, the derivative of f(x) is the quotient of an infinitesimal change in y over an infinitesimal change in x. Put more precisely, it is exactly the limit of the change in y over the change in x over smaller and smaller changes in x. The “dx” and “dy” notation just captures this limiting procedure and expresses it as an infinitesimal change in x or y instead.

“dx” as seen in integrals

Another place where "dx" is often seen is in integrals. Let's focus on definite integrals. What does "dx" mean in a definite integral?

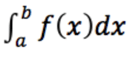
"dx" here is still an infinitesimal change in x. To see why it's there, we should think of the integral as a signed area and as the limit of Riemann sums. We recall that to compute a left Riemann sum of f(x) from x=a to x=b with n intervals, we let the following be true:

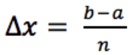
Then we take:

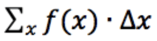
...where x takes values a, a + ∆x, a + 2∆x,..., a + (n - 1)∆x = b - ∆x.

Then, as we let n go to infinity, ∆x gets smaller and smaller, and the Riemann sum converges in value to the integral, which is the signed area under the curve f(x) between x=a and x=b. The below picture (from the Wikipedia article on Riemann sums) shows this convergence process:

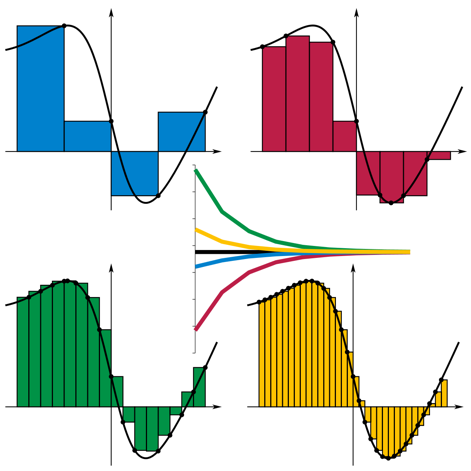
Another way to think about this is that in our integral, we are summing up infinitesimally thin rectangles with height f(x) and width dx to compute our signed area precisely.

Hopefully, the symbol “dx” is a little less mysterious now!