As a musician, I had always wondered why different instruments sound distinct from one another, despite being in-tune and playing the same note. Why is it so easy to distinguish someone singing a C major scale versus someone playing the same scale on the piano? Timbre, tone color, or tone quality of a sound are those characteristics separate from pitch or volume, and are usually described with intangibles: like warm cello, open organ pipe, bright trumpet, or tinny cymbal. It turns out that some of these elusive and seemingly-subjective characteristics may be rationalized quantitatively by means of the Fourier Series.
Well-made instruments vibrate in a way that accentuate integer multiples of the fundamental frequency – that is, the harmonics – while played. While every mechanical structure will have several natural frequencies that correspond to its internal vibration modes, they may not necessarily sound musical: it’s unlikely that your desk, chair, or door will exhibit a recognizable pitch when struck, and if it does, it will not sound musical. Musicians recognize tones with a 2:1 frequency ratio as an octave, 3:2 as a perfect fifth, 4:3 as a perfect fourth, 5:4 as a major third, etc. In general, if the frequency ratio between two tone scan be expressed with small integers, the combination sounds consonant and harmonious. Engineers, agnostic of musical background, will still denote the frequencies 2ω,3ω, ..., nω as “harmonics”, a nod to their importance in music.
Vibrations of a Guitar String
A well-made guitar string will vibrate at a fundamental frequency prescribed by its weight and tension:
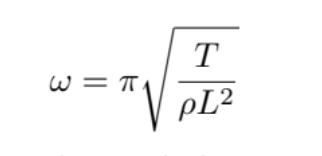
where T is the tension of the string, ρ is its mass per unit length, and L itslength. Note that this is consistent with our intuition about guitars and musical instruments in general. Tightening a string (increasing T) raises the frequency, which corresponds to tuning the guitar. Fretting a string (lowering L) also raises the pitch. While one may not easily changeρwhile playing the guitar, note that on most guitars, the strings tuned to a higher pitch are made with a narrower-gauge wire (loweringρ) despite having the same length and ideally similar tension.
While the equation above describes the lowest frequency that you would hear on the guitar string, plucking it will inevitably excite higher frequencies. Only certain frequencies are naturally excited though, and the nth frequency may be found via:
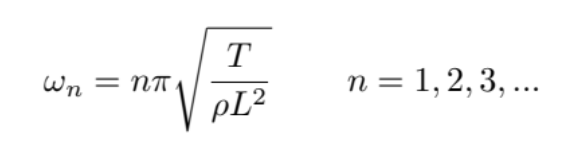
The equation above is backed up by mathematical theory developed in the 19th century, and agrees well with observation (Lord Rayleigh, Theory of Sound,1877). Strings make good musical instruments because of the miraculous fact that the overtone frequencies ωn of a pinned string are exactly integer multiples of the fundamental frequency, which naturally sound musically consonant and harmonious. Other instruments that can be shown to have this feature are violin strings, organ pipes, and the human voice. Not all mechanical structures will exhibit this particular relation between vibration harmonics: take your desk, for example. Does it sound musical if you hit it?
Note here that the frequency of the 2nd harmonic would be the frequency of a string of the same constitution, but half the length: L÷2. Likewise, the nth harmonic is the frequency of a string of length L÷n. This suggests that the shape of the nth mode of a plucked string assumes the shape sin(nπx÷L)(This may also be backed up by using more advanced mathematical techniques). This leads us to believe that the most general motion of a plucked guitar string is a weighted sum of the vibrations of all the different harmonics.
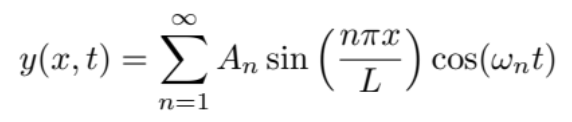
If you have ever played with a guitar, you may have noticed that it sounds different to pluck the string at the base, near the resonator, and at the 12th fret. Likewise, it sounds different to pluck the string with a pick and with your thumb. Let’s use this equation to rationalize the difference between these sounds.The weights An in the equation above are constant with time , and cosine of zero is 1. Therefore, we may model the sound of our string by imposing y(x,0) = ƒ(x),that is, matching the shape of the string to a chosen shape ƒ(x) at t=0. Thereafter, each mode vibrates at its own frequency while the relative weighting remains unchanged, where we can use An as a measure of the prevalence of the higher musical harmonics.
Without any help, picking an infinite sequence of numbers An to match an arbitrary shape ƒ(x) seems like an impossible task. Luckily, Fourier’s Theorem guarantees that we may approximate any function defined in a finite window – like the initial shape of our string ƒ(x), defined between 0< x < L – using a weighted sum of sines and cosines. Since our string is pinned at both ends, we can do so using only sines. Furthermore, Fourier’s Theorem gives us a closed-form expression for the An, the coefficients of the Fourier Series, which is:
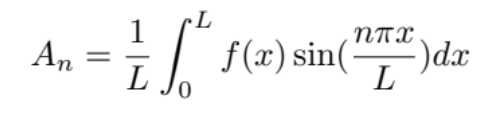
Hearing the Fourier Spectrum
Consider picking the guitar at the base of where the string is attached to the bridge. Let’s measure length in units such that L= 1 to simplify the arithmetic, and then our model of the initial string state as:
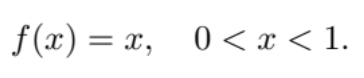 We may now directly evaluate the Fourier coefficients by computing the following integral:
We may now directly evaluate the Fourier coefficients by computing the following integral:
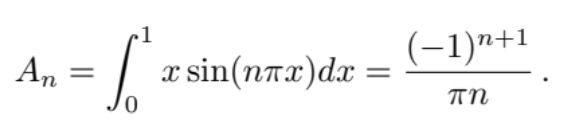
Convince yourself of this by applying integration by parts once using “u=x”,“dv= sin(nπx)” and noting that sin(nπ) = 0 and cos(nπ) = (−1)n+1.Now consider picking the guitar at the 12th fret. Let’s model this as the following function which also has unit amplitude. The following does the job:
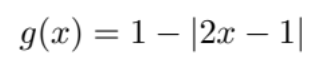
The fourier coefficients of this function would then be:
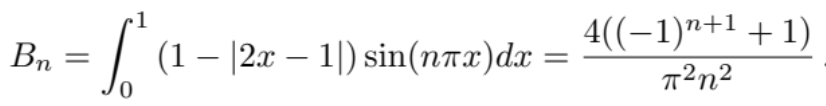 Finally, consider plucking the string with your thumb, as opposed to your nail or a guitar pick. To model the flat part of your finger, let’s pick the following quadratic function to represent this shape.
Finally, consider plucking the string with your thumb, as opposed to your nail or a guitar pick. To model the flat part of your finger, let’s pick the following quadratic function to represent this shape.
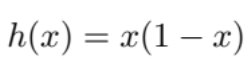
Convince yourself that this is flat at some point in the center of the string while remaining pinned at the endpoints 0 and 1. Likewise, the Fourier coefficients may be obtained as follows.
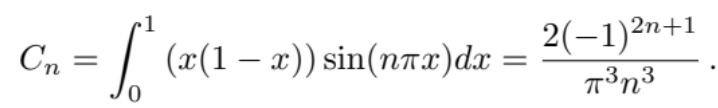
Now, let’s rationalize the difference between these three styles of plucking by examining the relative magnitude of the Fourier coefficients. First, let’s notice how the coefficients depend on n. Note that the largest coefficient of An,Bn, and Cn is always the fundamental pitch, n= 1. As n grows larger, the relative weight of the higher harmonics decays to zero, for each An is proportional to 1/n, 1/n2, or 1/n3, respectively. For large n, we have 1/n > 1/n2 > 1/n3, and therefore we have An > Bn > Cn for large enough n. This means that by plucking the string right at the base, we excite the maximum amount of high-frequency harmonics in the string, which is consistent to the distinctive “twang” you would hear if you try this at home. Likewise, if you pluck the string towards the center, you excite less higher harmonics, and if you use your thumb, even less still: consistent to our notion that playing a guitar with your fingers and thumb leads to a warmer tone color than using a pick.
You will also notice a distinctive tone color if you strike a guitar exactly at the 12th fret. We can rationalize this by noting that Bn and Cn are zero whenever n is an even number: only the odd harmonics are excited here. I always found that doing this sounds reminiscent of retro video game music, which quintessentially utilizes triangle - and square- wave synthesizers, which also contain only odd harmonics.
Ref: Fundamentals of Musical Acoustics, Arthur H. Benade (Dover)Theory of Sound, Lord Rayleigh (Dover)
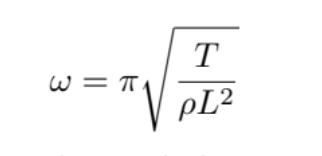
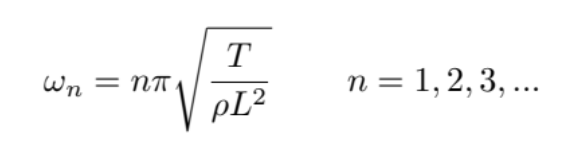
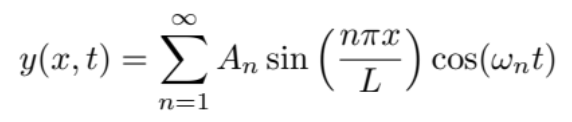
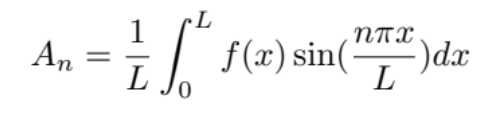
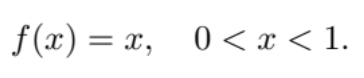
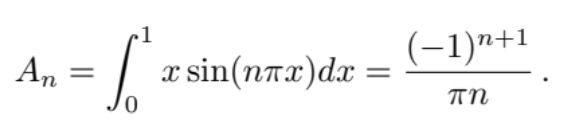
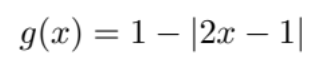
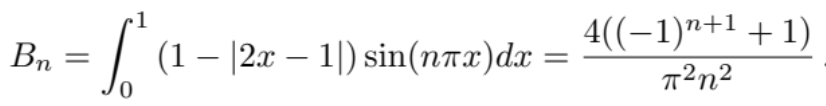
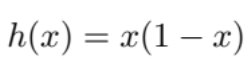
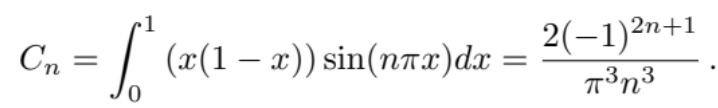
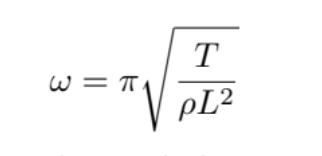
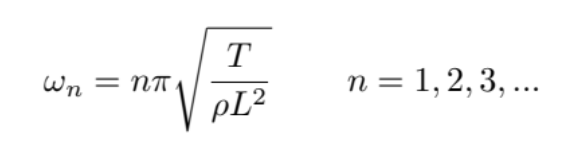
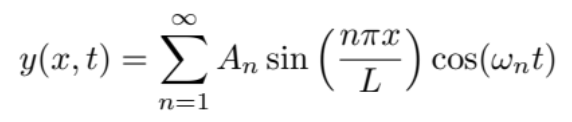
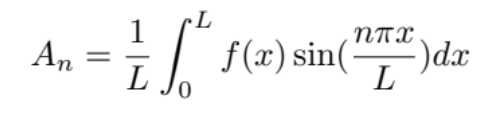
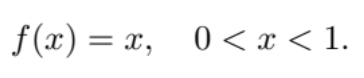
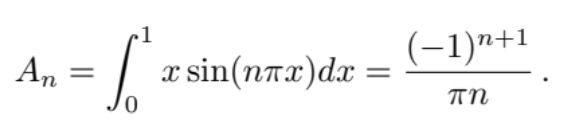
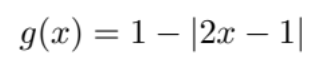
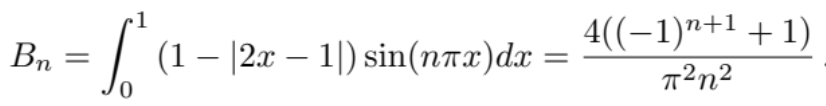
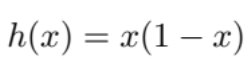
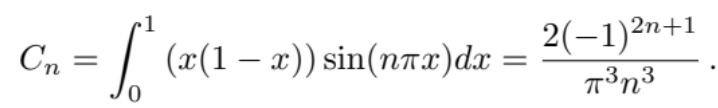


Comments