Comparing finite set sizes, or cardinalities, is one of the first things we learn how to do in math. From a young age, we can answer questions like “Do you see more dogs or cats?” Your reasoning might sound like this: There are four dogs and two cats, and four is more than two, so there are more dogs than cats. In other words, the set of dogs is larger than the set of cats; the cardinality of the dog set is greater than the cardinality of the cat set.
This reasoning works perfectly when we are comparing finite set cardinalities, but the situation is murkier when we are comparing infinite sets. Are there more integers or rational numbers? More rational numbers or real numbers? Are all infinitely large sets the same “size”? To answer these questions, we need a way to compare cardinalities without relying on integer counts like “two” and “four.”
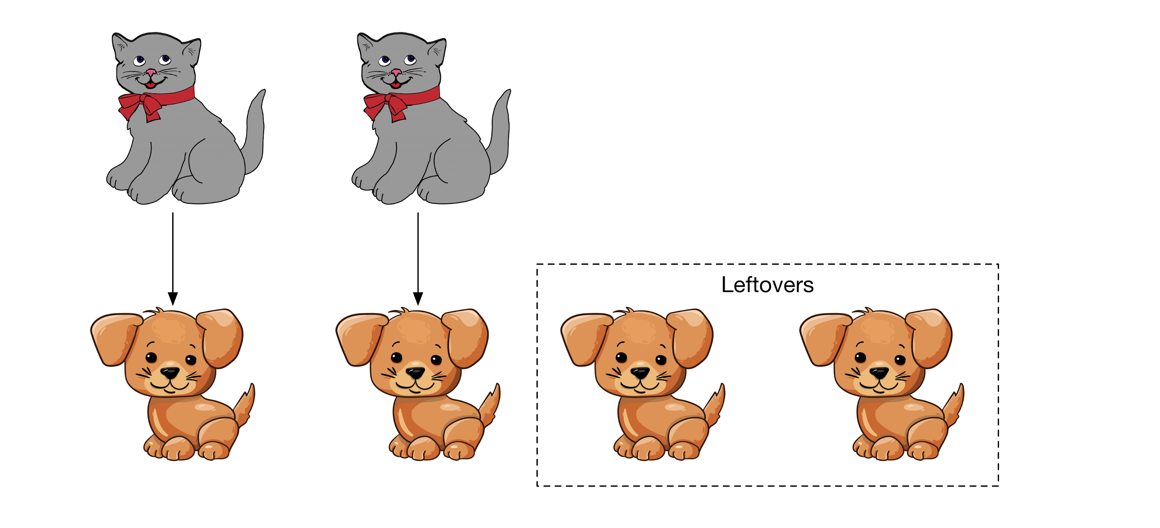
A different way to compare set sizes is to “pair up” elements of one set with elements of the other. Returning to cats and dogs, if we pair each cat with a unique dog and find that there are “leftover” dogs, we can conclude that there are more dogs than cats.
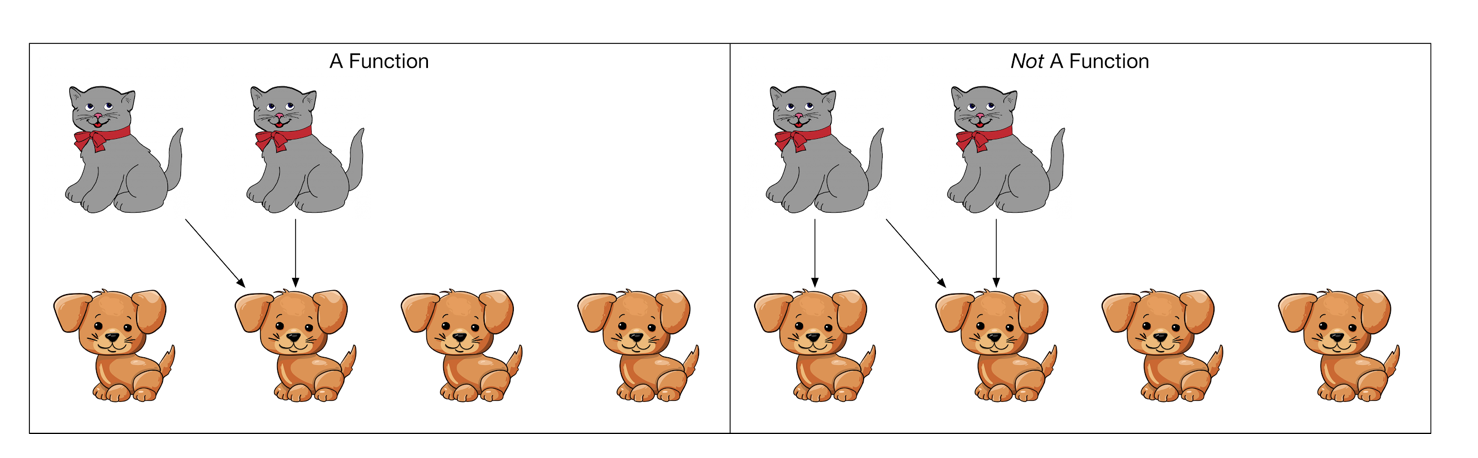
Another way to describe “pairing up” is to say that we are defining a function from cats to dogs. In a function, each cat is associated with one dog, as indicated by arrows. The figure on the right below is not a function because the first cat is associated with more than one dog.
If a function associates each input with a unique output, we call that function injective.
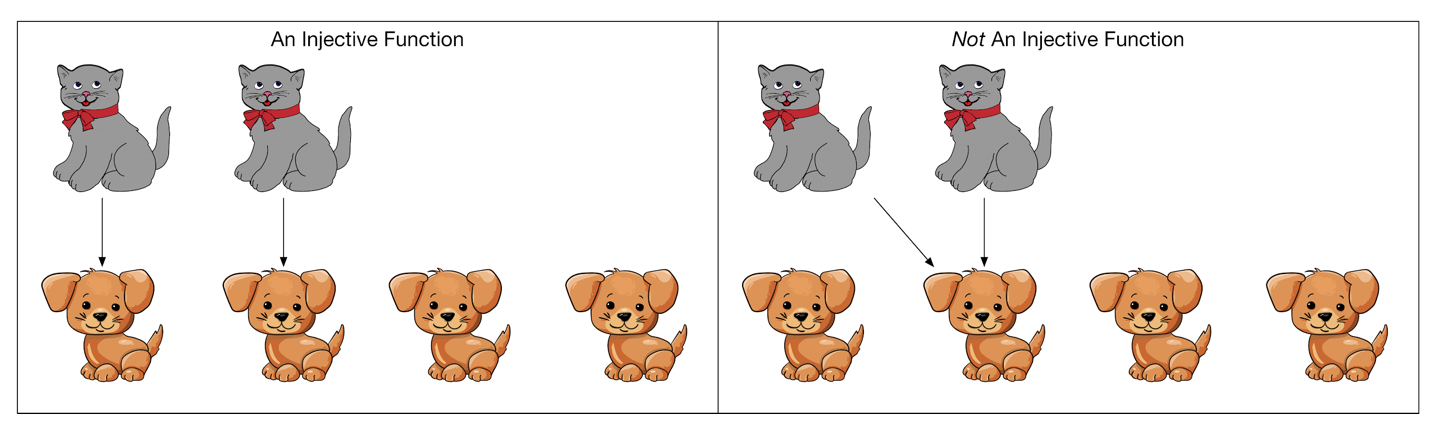
Since we have found an injective function from cats to dogs, we can say that the cardinality of the cat set is less than or equal to the cardinality of the dog set. Take a moment to convince yourself that this makes sense.
In formal math notation, we might write: if f : A → B is injective, then |A| ≤ |B|. In other words, if there is some injective function f that maps elements of the set A to elements of the set B, then the cardinality of A is less than or equal to the cardinality of B.
Let’s add two more cats to our running example and define a new injective function from cats to dogs.
Now we can also define an injective function from dogs to cats.
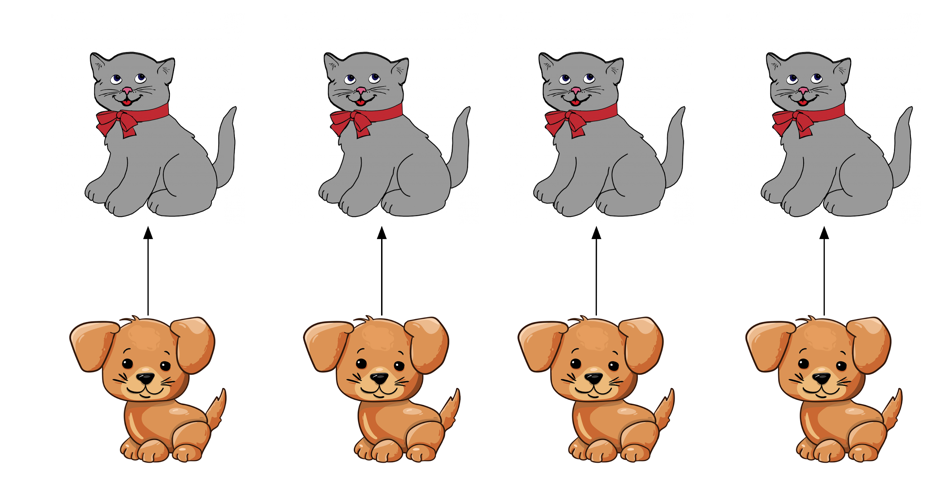
We see that each dog is associated with exactly one cat, and each cat with one dog.
Since we have found an injective function from cats to dogs, and an injective function from dogs to cats, we can say that the cardinality of the cat set is equal to the cardinality of the dog set. We might also say that the two sets are in bijection. In formal math notation, we would write: if f : A → B is injective, and g : B → A is injective, then |A| = |B|.
Now we have a recipe for comparing the cardinalities of any two sets. If we can find an injection from one to the other, we know that the former is less than or equal; if we can find another injection in the opposite direction, we have a bijection, and we know that the cardinalities are equal.
The important and exciting part about this recipe is that we can just as well apply it to infinite sets as we have to finite sets. For example, we can ask: are there strictly more integers than natural numbers? The natural numbers (1, 2, 3…) are a subset of the integers (..., -2, -1, 0, 1, 2, …), so it is tempting to guess that the answer is yes. But in fact, we can define an injective function from the natural numbers to the integers by mapping odd numbers to negative integers (1 → -1, 3 → -2, 5 → -3, …) and even numbers to positive ones (2 → 0, 4 → 1, 6 → 2). From the existence of this injective function, we conclude that the sets are in bijection; they are the same cardinality after all.
A surprisingly large number of familiar infinite sets turn out to have the same cardinality. (Can you compare the natural numbers and the rationals (fractions)?) This begs the question: are any infinite sets strictly larger than any others? In the late 19th century, a German mathematician named George Cantor rocked the math world by proving that yes, there are strictly larger infinite sets. One example is the set of real numbers (infinite decimals). Cantor’s Theorem builds on the notions of set cardinality, injective functions, and bijections that we explored in this post, and has profound implications for math and computer science.
Comments