Fictitious forces such as the centrifugal force are fake forces – they don’t really exist! However, fictitious forces are helpful when working in non-inertial reference frames (a fancy term for reference frames that are accelerating, like when we use the rotating Earth as a reference frame). In these frames, F = ma doesn’t hold, and you’ll need to include fictitious forces with the real forces to explain why your object is accelerating (or not accelerating).
What is centrifugal force?
The centrifugal force is a fictitious force that appears to act on objects in a rotating reference frame, pushing them away from the center of rotation.
Centrifugal and centripetal force are not the same!
Centrifugal force is a fictitious force acting away from the axis of rotation that appears only in a rotating reference frame; centripetal force is a real force acting towards the center of rotation that causes objects to undergo circular motion (for example, the gravitational force on an orbiting satellite).
The best way to understand centrifugal force is with an example.
Imagine that a satellite that stays in the same spot over Earth’s surface as it orbits the Earth.
Let’s compare how two observers, Observer A and Observer B, would view this satellite.
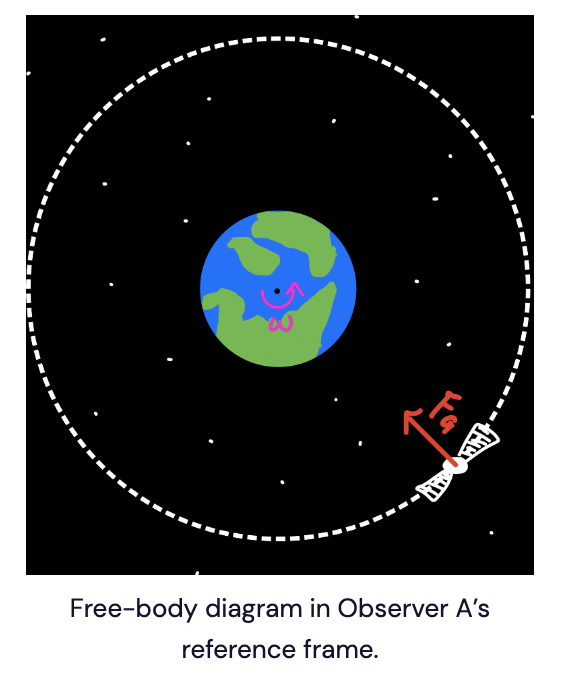
Observer A in outer space
- When Observer A looks down at Earth, they see both the satellite orbiting Earth and the Earth rotating.
- Earth’s gravity is the only force acting on the satellite. This force pulls the satellite toward Earth, which makes sense, since the satellite is undergoing circular motion and therefore requires constant acceleration. F = ma holds!
- Therefore, we say that Observer A is an inertial reference frame (”inertial” because inertia holds – the satellite accelerates only because there is a net force acting on it).
Observer B on Earth
- Observer B is standing on Earth; when they look up at the sky, the satellite looks like it’s not moving.
- Yet Earth’s gravity is still the only force acting on the satellite.
- But wait! How can there be a net force acting on the satellite, yet it doesn’t seem to move? It seems that F = ma doesn’t hold. And that’s because it doesn’t: Observer B is in a non-inertial reference frame (specifically the rotating reference frame of Earth) where Newton’s second laws don’t hold.
But wait again! What if there was a force that was exactly equal in magnitude to gravity, but pointed in the opposite direction? Then, there would be no net force acting on the satellite, and F = ma would accurately predict that the satellite doesn’t move. Let’s call this fake force the centrifugal force.
If it’s helpful, according to the Merriam-Webster dictionary, centrifugal is defined as “proceeding or acting in a direction away from a center or axis”.
 The centrifugal force may be fake, but from Observer B’s perspective we need this fictitious force because it’s not immediately obvious that they’re in a non-inertial reference frame; from their perspective, it looks like there’s a centrifugal force acting on the satellite that keeps it from crashing into the Earth. Adding a fictitious force allows us to “rescue” F = ma.
The centrifugal force may be fake, but from Observer B’s perspective we need this fictitious force because it’s not immediately obvious that they’re in a non-inertial reference frame; from their perspective, it looks like there’s a centrifugal force acting on the satellite that keeps it from crashing into the Earth. Adding a fictitious force allows us to “rescue” F = ma.
Magnitude and direction
From this example, we can see that a centrifugal force must be equal in magnitude to the acceleration needed for uniform circular motion and opposite in direction. Fcentrifugal = mw2r, where positive is taken to be toward the center of rotation. Note that we're using our intuition here, not rigorous knowledge.
Generalizing this approach
To identify the centrifugal force in any situation: pick an object, choose your reference frame, and then ask yourself two questions:
- Is the object accelerating?
- Remember that acceleration can be a change in speed OR direction (or both).
- Given the net force acting on the object, should it be accelerating?
- If the net force is 0, then it should not be accelerating.
- If the net force is not 0, then it should be accelerating.
- Are the answers to questions 1 and 2 the same?
If the answers are the same
- F = ma works.
- By definition you are in an inertial reference frame.
- No fictitious forces of any kind are needed to explain the object’s motion.
If the answers are different
- F = ma does not work.
- You are in a non-inertial reference frame.
- Without a fictitious force, there’s nothing to explain why the object is accelerating when it shouldn’t be, or why it’s not accelerating when it should be.
- Therefore, we need to include a centrifugal force equal in magnitude to the centripetal acceleration and opposite in direction to explain the object’s behavior.
As we’ve seen, the centrifugal force is a fictitious force that arises for uniform circular motion. We can imagine more complicated scenarios (perhaps the satellite is rotating at a different speed than Earth, or Earth’s rotation is not constant) that require additional fictitious forces (and additional mathematical complexity).

Comments