Basic Data Analysis Topics
Do not underestimate the data analysis section of the GRE. It covers a lot of material, one of which is probability (which is an advanced topic) and that isn't taught very well in school. But probability is also a very small percentage of the test, so think hard about whether or not you want to spend time on it if you have limited time to study. A lot of my students come to me and say straight off the bat that they want to start with probability. They know they are weak in it and want to attack it right away. But 100 percent of the time, I find that it is not the probability that is costing them valuable points, but basic arithmetic, word problems, or table reading. So don’t underestimate the basic topics!
Reading tables
- Not all axes are created the same, so make sure they know to focus on the axis and the units of increase. Make sure you read the titles. Is the table showing you a percentage or an actual number? Which part of the graph/table is MOST essential? Sometimes the question is only asking you to read one column, so you can ignore the rest of them!
- Questions associated with a table are time consuming but easy. Usually 1-2 graphs will come with 3-4 questions. Some students skip these because they think it will take too much time but before you do, remind yourself, these questions are EASY and low hanging fruit. If you aren’t getting the harder questions right anyway, you might be better off spending your time on these. Remember to spend your time wisely.
Statistics
- GRE statistics questions are fairly rudimentary. They test if you understand the very foundational conceptions of statistics. They will NOT, I repeat, NOT cover tests of significance (z-test, t-test, anova, etc, etc, forget I am even mentioning these)
- You'll need to be able to draw out a normal distribution curve and point to the median, mean, mode, standard deviation, and range.
- Medium, mean, mode: can’t emphasize this enough. Make sure you know which are used when and why.
- Know formulas for the mean and how to find the median
- 95% of the data is covered with 2 standard deviations from the mean
- GRE statistics tests what happens when the dataset changes (such as adding in another outlier).
- For example, what happens with the data skews right or left? In a normal distribution, mean=medium, but what about in other cases? What happens to range and SD when another item is added?
- The reason the GRE likes to test changing data is because statistics run our world. You open a news article and chances are there are some stats in there. Chances are the person writing the stats is banking on readers understanding somewhat but not entirely. I once had a math professor say that stats are like a bikini, what it reveals is revealing but what it hides is essential.
- For example, the median is less affected by an outlier than the mean. If a company has outlying data that it wants to hide, it will most likely report the median and call it the average (which is still perfectly legitimate, an average is anything that summarizes the data) but see how deceptive the company is being? See how a layman reader might not catch on? Knowing how the skew affects data measurements is an important skill for you to learn as an informed citizen of the world!
Advanced Probability Topics
So now we got ourselves to the dreaded probability. To ease students in, I usually start talking about blackjack. First because I like blackjack and second, it is a good way to show you the importance of probability. So, let me ask you a question. What is the difference between an odds and a probability? This is a key concept to understand. Go to any blackjack table and see that the signs says odds of winning are 2:3, which doesn’t sound so bad, right? What if the sign had said, probability of winning is 40%? Would you see it differently? These two numbers are getting at the same concept actually. A 2:3 odds is the same as a 40% chance of winning. Going back to what we learned in arithmetic, odds are a ratio. Probability is a proportion.
Below are some other probability topics that come up.
Factorials
- Know what it means. 5! means 5*4*3*2*1. 20! means 20*19*18…...3*2*1. Now factorials can get scary when it comes to calculations. If you see something like 15!, do not, I repeat, do not try to calculate it. Chances are there is some way to whittle down everything in the factorial so you are only multiplying a few numbers in the end. If you have 10!/5! you only need to multiple 10 through 6.
Combinatorics and permutations
- They are essentially the same thing. Don’t let anyone tell you differently! In one (permutations), order matters, in another (combinatorics) order does not. A combinatoric is a permutation taken one step further. For both, I recommend doing ‘slots.’
- An example: how many ways are there to order 4 people? To do this question, draw out 4 slots and then ask yourself how many people are in this slot, and so on. You will find that at first there are 4, then 3, then 2, then 1. So the answer is 4! What you just did is a permutation.
- Another example, how many ways are there to choose 2 people out of 4? Whenever you see the word choose in a problem, it is asking for combinatorics. Here you only have 2 slots and in each will be 4 and then 3. But this is counting all the redundancies. That is, selecting person A then person B is a different group than selecting person B then person A. But those two options are the same group. So to get rid of redundancies, you have to divide out how many ways there are to order 2 people, which is 2. So the answer to this question is (4*3)/2=6.
- Whenever you see the word ‘choose’ in the problem, as in ‘choose 2 members’, the question is Combinatorics.
Overlapping sets
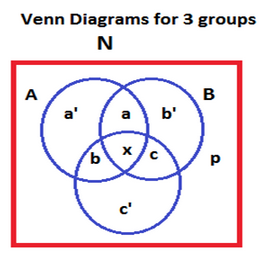
- This is not quite probability but it is probability adjacent. I have seen both venn diagram and table strategies used here.
- I prefer using a venn diagram because I am a more visual learner and I like to be able to fill in sections of the venn diagram with what I know.
- Below is a venn diagram for 3 groups, A, B and C. When the GRE does overlapping sets, they like to do 3 groups because it can get complicated fast. Just be able to fill in venn diagram with as much information as you can.
- For example, X is the number of people in all three groups. A’ is the number of people ONLY in the a and no other group. A is the number of people in both A and B.


Comments