
Sitting at the cross-roads of mathematics, statistics, and computer science, the emerging field of data science (ranked by many as the top career in the US) seems daunting to those still developing strong technical skills. At the same time, a host of dynamic and highly-efficient libraries give coders the power to treat complex areas like machine learning as a black box.
There is, however, middle ground: an intuitive understanding of mathematics that makes that box somewhat less opaque. Moreover, it suggests an end-goal for students learning mathematics at all levels: that there is something important to be gained studying math quite aside from the computations and the proofs.
Example I – Calculus and Optimization
Machine learning is concerned, generally speaking, with the task of teaching computers to learn from data without constant human oversight. In practice, the computer is programmed with a vague model of learning, and fills in the specifics in accordance with the data it is given. And how does the program know when it has succeeded or failed? The scientist provides a function that measures the explanatory power of the computer’s learning, and charges the computer with optimizing it. Then the program runs and runs until it arrives at a conclusion which provides the most explanatory power.
One of the many challenges in implementing this strategy is the problem of realizing when one has stumbled on an optimal solution. Should the computer decide on the best hypothesis only after considering all the alternatives? In practice this is impossible – such programs may take millions of years to run! Here, calculus provides an answer – at an optimal solution the derivative of the learning function will be zero. Thus, all we need to do is start with a poor solution and tinker with it, decreasing the derivative until we arrive at zero. So far, so good. However, there is still a problem with this approach. Can you guess what it might be?
The answer is: although the derivative is zero at the optimal solution, having a zero derivative does not mean your solution is optimal. Such a solution may only be locally optimal, i.e. better than only the nearby alternatives.
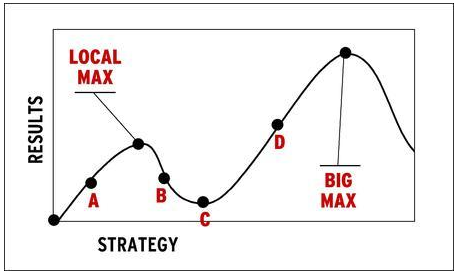
Indeed, what can often happen is that your program gets “trapped” in a local optimum, never realizing that although your strategy is better than similar alternatives, it may be far inferior to vastly different ones. In practice, dealing with this problem is tricky and case-specific. Someone interested in such a data problem does not necessarily need to have a mastery of complex optimization techniques. But they do need to understand why this approach has a tendency to produce sub-optimal results and how that relates to the shape of the data and the optimization function, as drawn above. Such an intuitive appreciation can inform them as to when, if necessary, they need to reach for a more sophisticated code module.
Example II – Linear Algebra and Dimensionality Reduction
Another major challenge in machine learning is dealing with the problem of having too many features. For example, customers’ decisions may be affected by only a small handful of variables, but the company collected information on many more. Or perhaps some variables are so closely related that recording all of them is unnecessary. An abundance of variables makes computation difficult and obscures the underlining meaning present in the data. One common approach to get around this is dimensionality reduction¸ which amounts to the judicious throwing away of unnecessary variables. This is often accomplished via Principal Component Analysis, or PCA. A foray into the mathematics of PCAs requires an understanding of linear algebra, which, while ideal, is not something one can always assume.
So, here is an intuitive explanation. Put simply, PCA isolates the most import variables by computing how much explanatory power would be lost if we forgot about them. Suppose that I am analyzing a sector of the stock market and companies A,B, and C are all performing virtually identically. I could ignore about any two of them and not lose information from my data set.
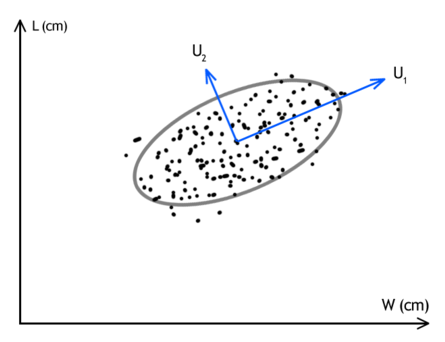
The picture above is a more common example. The collection of points represents my data set; U1 and U2 are two distinct combinations of the underlying variables. If I had to choose one of U1 or U2 to record and another to discard, clearly U2 would have to go, since this combination does not vary as much over the whole data set and is less useful in distinguishing my data points. In practice there may be hundreds and thousands of variables, and since we cannot visualize things as we just did, we use linear algebra and statistics to automate the process.
The advantage of having such an intuitive understanding, even without all the technical details, is that it helps appreciate any subtleties that may develop. This explanation makes it quite clear that the process of PCA is very sensitive to the correct choice of units used. Measuring one company in US dollars and another in Ruble would throw off the scales and produce poor results, and a scientist who realizes this is likely like to accidentally overlook it.
Mathematics as Intuition
The purpose of the above two examples is two demonstrate that underlying every technical aspect of mathematics is an intuition that drives it. This intuition is often more accessible than the associated formalism, and in practice the former can sometimes be substituted for the latter. Simply having the right picture in mind can transform a black box into a tool to be wielded creatively.

Comments