Demystifying the cross product

The cross product is ubiquitous throughout linear algebra and vector calculus. It plays a major role in transformations of coordinate systems and is intimately related to the determinant. In fact, its definition in linear algebra courses is often given in terms of the determinant, which can seem mysterious and arbitrary. In this post, I want to demystify the cross product by defining it formally and computing it from scratch.

The cross product

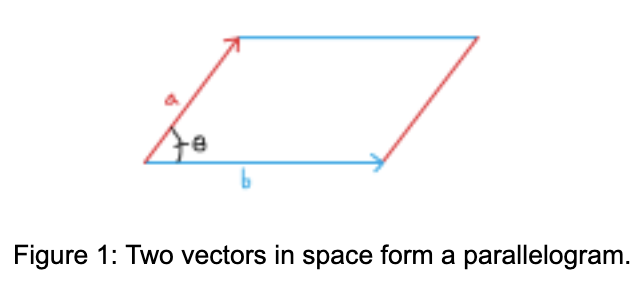
The cross product is a vector operation that occurs between two vectors in a 3D space. It is defined as

a × b = |a| |b| sin(θ)n 

for vectors a and b and θ the angle between them. |a| denotes the magnitude of a. The vector n has a magnitude of 1 and points in one of the two directions that is perpendicular (at a right angle to) to both a and b. Which of those two it points to depends on the right hand rule: imagine a as your index finger and b as your middle finger of your right hand. Then your thumb, as it points directly up, is the direction of n. From this definition it’s not exactly clear how to compute it, but that will be covered in the next section. One important thing to notice is that the right hand side of this equation is equal to the definition of the area of a parallelogram. This means that the magnitude of the cross product of two vectors is equal to the area of the parallelogram spanned by those vectors.

Computing the cross product

In case you aren’t familiar with the concept of unit vectors, think of them as a set of vectors that each point a cardinal direction in vector space and have a magnitude of 1. In Cartesian coordinates, they are (1, 0, 0), (0, 1, 0), and (0, 0, 1). They are typically denoted by i, j, and k, and they point in the direction of x, y, and z, respectively. 

Any vector in Cartesian space can be rewritten in terms of these unit vectors: 

(a, b, c) = ai + bj + ck 

It is important to notice that because the x-, y-, and z-axes are perpendicular to each other, so are i, j, and k. Using the definition, we can compute the cross product of these vectors with each other: 

i × j = k 

j × k = i 

k × i = j 

where we have used the fact that sin(90°) = 1 and the magnitude of a unit vector equals 1. Remember that the direction of the cross product depends on the right hand rule, so if you swap the order of the two vectors being crossed, the answer will be the same but with a negative sign: 

j × i = −k 

Using this, we can now compute, with a bit of effort, the cross product of any two arbitrary vectors. 

Suppose

a = a₁i + a₂j + a₃k and b = b₁i + b₂j + b₃k.

Then 

a × b = (a₁i + a₂j + a₃k) × (b₁i + b₂j + b₃k) 

We can expand this using the distributive property: 

a × b = a₁b₁(i × i) + a₁b₂(i × j) + a₁b₃(i × k) 

+a₂b₁(j × i) + a₂b₂(j × j) + a₂b₃(j × k) 

+a₃b₁(k × i) + a₃b₂(k × j) + a₃b₃(k × k) 

= (a₂b₃ − a₃b₂)i + (a₃b₁ − a₁b₃)j + (a₁b₂ − a₂b₁)k 

And there we have it. This is the simplest general form of the cross product of two vectors, and it is equivalent to the often-given definition that involves determinants. Note that we have used the fact that the cross product of a vector with itself is always zero, because the angle between a vector and itself is zero, and the sine of zero equals zero.