In this post, we’re going to prove the most famous formula in all of science, E = mc^2! We’ll do this using a simplified version of Einstein’s original 1905 proof. In this post I will assume that you are familiar with special relativity and Lorentz transformations.
Consider a box of mass m which is at rest. At a certain moment, it spontaneously releases two photons of wavelength λ moving in opposite directions.
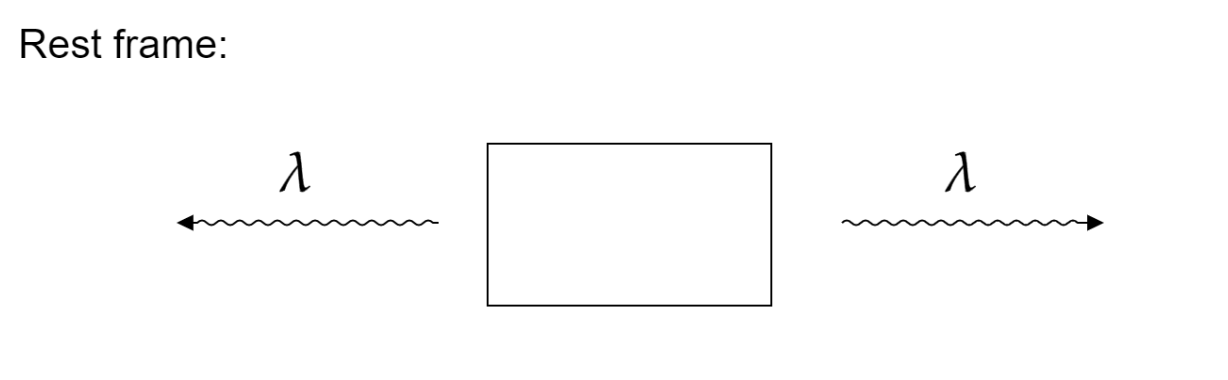
The energy of a photon is given by
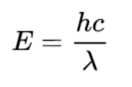and the momentum of a photon is given by
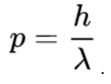This means that, in order for energy to be conserved, the box must lose two photons worth of energy:
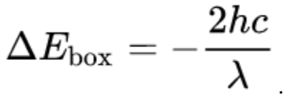Let’s now consider this exact same scenario in another reference frame. Namely, let’s consider the reference frame where the box is moving with some velocity v.
The wavelengths of the two photons will be different in this reference frame. In fact, one of the photons will be “blueshifted” (its wavelength will shrink) and the other photon will be “redshifted” (its wavelength will expand). Let’s derive a formula for how the wavelength of a photon is changed when we shift reference frames.
To do this, notice that the equation of a wave moving to the right is
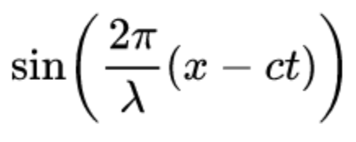A photon is a wave of light, and is more or less described by the above equation. (We will not worry about what is waving, or what is the amplitude of this wave. All we need to know is that a photon is some sort of wave, as above.)
We can use the formula for a Lorentz transformation to express the old coordinates, t and x, in terms of the new coordinates t’ and x’.
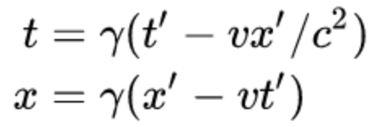Let us now re-express the quantity x - ct, which appears in our equation for the wave, in terms of the new coordinates x’ and t’. In order to do this, we simply plug our above expressions for t and x into the expression x - ct. We then find, after a bit of algebra,
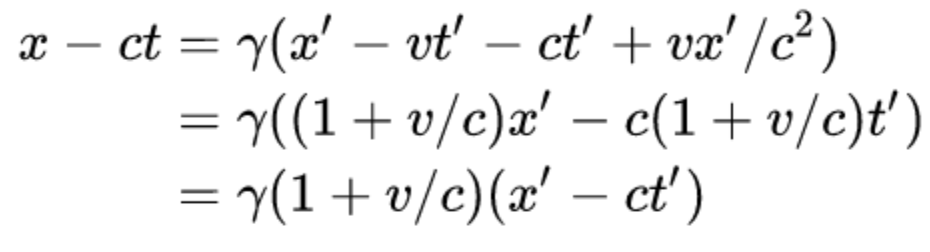
Plugging this into our expression for a wave, we get
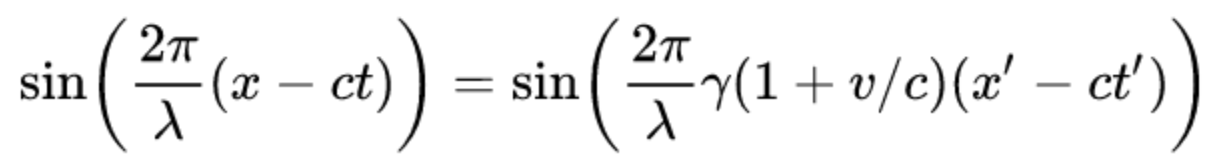If we stare at the right hand side of the above equation, we realize that the wavelength λ’ in the new frame is simply equal to
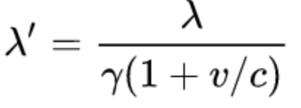which is what we wanted to show.
Now, from here on out, we’re going to make a simplifying approximation. We’re going to assume that our velocity v is much smaller than c. Therefore, we’re going to drop all terms which are second order in v. For instance, when we do this, the Lorentz factor γ is approximately equal to 1. This is because if we do a Taylor expansion, we find that the first non-trivial correction to γ is second order in v and can be ignored:
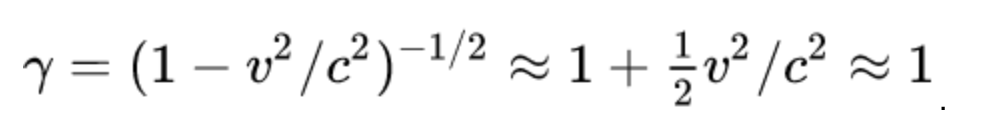Using this first order approximation, we therefore have that the momentum of the right-moving photon is equal to
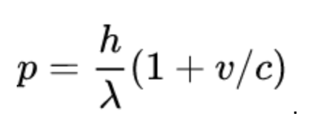
For the left moving photon, we have to modify this expression slightly. We have to switch v with -v because the photon is moving in the opposite direction of v, and we have to put an overall minus sign in front of the expression because the photon is moving in the other direction. All in all, the momentum of the left-moving photon is
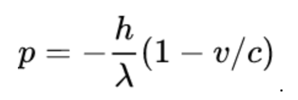
A picture of the situation is as follows:
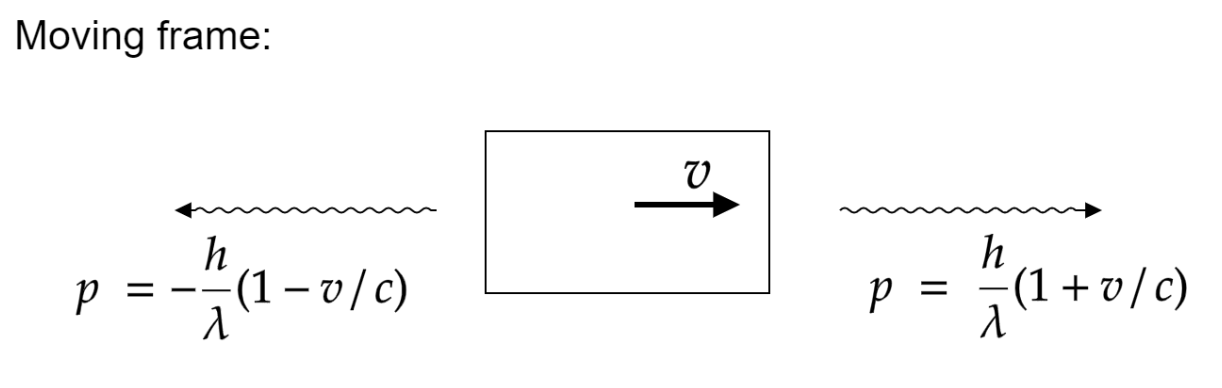
Therefore, the combined change in momentum due to the emission of the two photons is
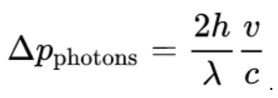Furthermore, because momentum must be conserved, the change in momentum of the box must be equal to
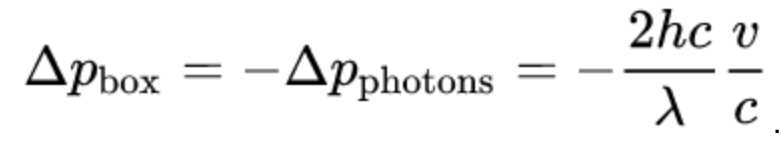
We are nearing the punch line.
Notice that, before and after the box emits the photons, it must be traveling at the v, meaning its velocity doesn’t change. (This can be seen by remembering we are looking at our stationary box in a moving reference frame.) Recall that the momentum of the box is equal to p = mv. (This formula for the momentum of the box is actually modified for velocities comparable to c, but because we’re only concerned about terms to the first order in v, we don’t have to worry about that and can use the non-relativistic formula.)
Therefore, because the momentum of the box must change after the photons are emitted, and because the velocity must stay the same, we can conclude the mass of the box must change!
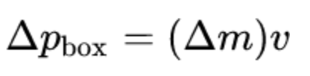This is a mind boggling result!
Equating the above two expressions, we know the mass must change by exactly
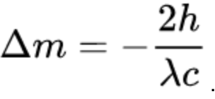We are almost done! If we massage this formula a little, we can re-express the change in mass in terms of the change in the rest energy of the box.
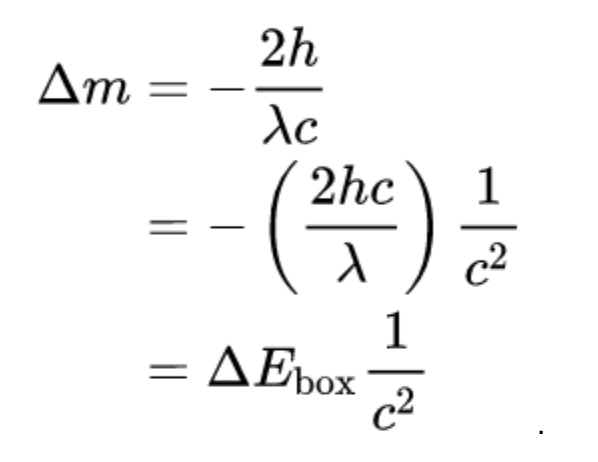
Therefore,
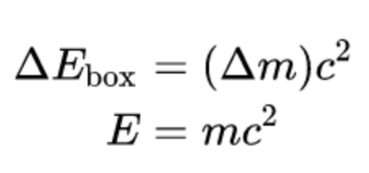
and we are done!
Comments