You started your electricity and magnetism course and now all you hear about are potentials, potential energies, fields, and forces. It’s overwhelming. The purpose of this post is to help you understand each of these quantities and how they are related.
Potential and Potential Energy
Let’s consider an isolated particle with charge Q. How should we describe the electrical effect it has on the space around it? The first thing we do is calculate the electric potential V (also denoted ɸ) created by this particle. Knowing the potential will help us figure out what happens if more charged particles come in its vicinity. More on that later. The formula below tells us how to compute the electric potential created by our particle.
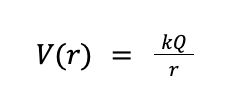
Look familiar? All this equation says is that, at a distance r away from the particle, the potential is proportional to Q and inversely proportional to r. Electric potential is measured in Volts and the constant k in the formula is just a constant of proportionality to make sure the units come out correctly. The numerical value of k will be given to you as needed or you can search for “Coulomb's constant” to find it.
Great! Now we know how to calculate the electric potential. But how does potential energy enter into this discussion? The potential energy U tells us about the energy associated with the interaction between charges. Therefore, to understand the potential energy we need to think about more than one charge at a time. Suppose there is a second particle with charge q that is a distance r away from the original particle above. The potential energy between the two particles is found by multiplying the potential V(r) by the new charge q.
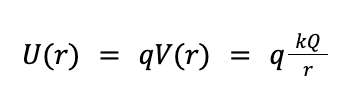
Simple enough. Potential energy grows in magnitude as q times Q gets bigger (more highly charged particles) and it gets closer to zero as the particles get farther away from each other (r becomes larger).
In summary, we see that a charged particle will create an electric potential. We use this potential to figure out the potential energy created when another charged particle is nearby.
Electric Fields and Forces
All this talk about potential and potential energy is still abstract. At the end of the day we care about how objects move and the forces acting on them. How does one charged particle cause another to move? A fundamental principle of electricity and magnetism is the following: electrical forces point in the direction of greatest decrease of electrical potential energy. In other words, electrical forces cause charges to move in such a way that the potential energy between them is minimized. What does that mean for our two particles of charge q and Q? Recall the potential energy between them is
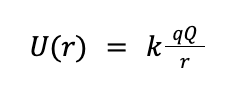
Let’s suppose both q and Q are positive charges. What will happen? In order to minimize the potential energy U, r will increase and the particles will get farther apart. Like charges repel! The magnitude F of the repulsive force is given by Coulomb's law.
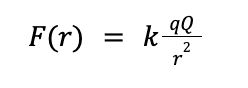
But what mediates electrical forces? Since the particles never actually touch, how do they exert forces on each other? You guessed it. Electric fields. Every charged particle creates an electric field. Analogous to how electric forces point in the direction of greatest potential energy decrease, electric fields point in the direction of greatest electric potential decrease. So for our particle of charge Q with potential
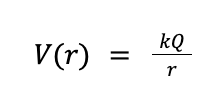
the electric field it creates will point in the direction which minimizes V. For positive Q that means the electric field will point in the direction of increasing r (i.e away from the particle). The magnitude of the electric field E created by a charge Q is given below.
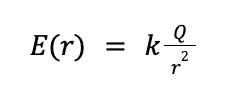
Notice how similar the electric force-electric field relationship is to the potential energy-potential relationship.
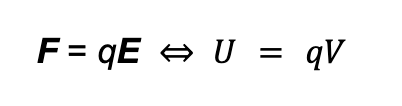
The major difference between the two sets of quantities is that electric forces/fields are vectors so they have a magnitude AND point in a particular direction while electric potentials/potential energies are just numbers. It’s often easier to calculate the potentials first and then use the minimization principles to determine electric forces/fields.
Wrapping up
When we want to figure out what kind of effect an electrically charged particle has on its surroundings we calculate its electrical potential. Once we know the potential we can figure out how much energy will be stored in the system if we bring another charged particle nearby. Using the fact that electric forces act in the direction which minimizes potential energy we can also figure out how particles will move as they interact with one another.
It seems like there are several different ideas to think about but there aren’t really. Just remember the relationship between potential and potential energy, and keep in mind the minimization ideas from above. If you do those two things, you will see how all the different quantities fit together. Good luck!


Comments