Escape velocity is the speed an object needs to escape the gravitational influence of another object. Here, we explain escape velocity, derive the right equation, and discuss what this equation does (and doesn’t tell us) about how objects actually move in space. For example, how fast would you have to throw a tennis ball for it to fly off into space and never return?
What is escape velocity?
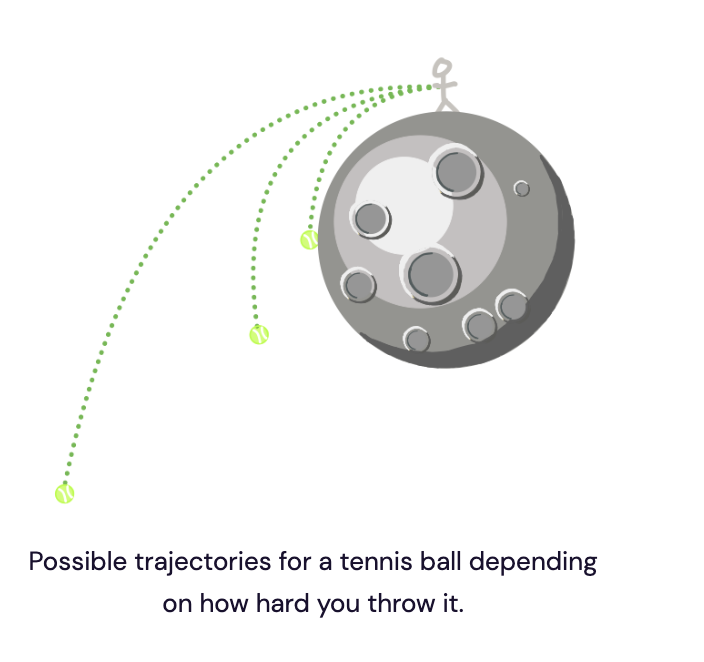
Imagine you’re on the surface of the Moon. You throw a tennis ball straight up. It comes back down.
Now you throw it again, but faster. It goes higher, stays in the air longer, but eventually comes back down.
Now imagine that Superman is on the Moon. He throws the tennis ball, only he’s so strong that the ball goes up aaaand up aaaaaaaaand up and just keeps on going! The Moon’s gravity isn’t strong enough to pull it back down.
Superman's tennis ball has enough energy to leave the Moon's gravitational influence entirely.
That means there must be a special speed in between the super slow tennis ball you threw and the super fast tennis ball Superman threw:
- Any slower than this speed, and the ball will come back down (even if it takes a while)
- Any faster than this speed, and the ball will never come back
Let’s call this special speed the escape velocity, and let’s find it! As we’ll see, the equation for escape velocity applies to all objects, but for now let’s focus on a tennis ball on the Moon.
Q: Aren’t speed and velocity different? Shouldn’t it be called escape speed?
A: Yes and yes. Speed is a scalar (does not have a direction), while velocity is a vector (has direction). Unfortunately, once upon a time somebody somewhere called this a velocity, so now we’re all stuck calling it that.
Finding escape velocity
To find escape velocity, let’s think about what happens when you throw a ball straight up.
- At the moment of release, the ball is moving. Therefore, it has kinetic energy.
- At its apex, the ball is no longer moving (for just a moment). Therefore it has no kinetic energy.
Therefore, throwing a ball converts kinetic energy to gravitational energy. Good ole’ conservation of energy! When you throw the ball, it will keep rising until all its kinetic energy has been transformed to gravitational potential energy.
The kinetic energy it starts with needs to equal the gravitational potential energy it ends with!
So what happens if we throw the ball faster?
It has more kinetic energy at the start, which means more energy can be transformed to gravitational potential energy. Therefore, the ball flies higher, but eventually it comes back.
But what if it didn’t?
What if the ball went so far away it kept going? What if it flew infinitely far away? How much kinetic energy would the ball need to fly infinitely high and never come back?
Well, if energy is conserved, then the ball needs however much gravitational potential energy a ball possesses at infinity. Aha! Conversation of energy suggests an equation that will allow us to solve for the escape velocity: the total change in kinetic energy and potential energy is zero.
A note about infinity
Thinking of escape velocity as the velocity needed to get to an infinite distance is NOT an intuitive concept (or at least not to me).
Here’s one way to think about it: we could replace “infinity” with “really really really far”, and all of our reasoning would still be valid. But math knows how to work with infinity.

An important goal of physics is to come up with theories that can accurately explain and predict what happens in real life; we then use experiments to test these theories. Mathematics is a very effective tool in helping physicists develop testable explanations and hypotheses for the natural world.
Instead of saying the escape velocity is very very fast, math (as we’ll see) allows us to precisely define the speed.
In short, we use infinity here because it aligns with our intuition, and the mathematical tools around infinity allow us to derive a precise equation that we can test. But this also means that the math could spit out an answer that’s complete nonsense! After all, there’s no reason that the real world has to align with our math, especially if one of our underlying assumptions in setting up the math was incorrect. And indeed infinity does cause trouble in other areas of physics (like renormalization in quantum field theory).
For now, let’s go ahead and assume this reasoning holds (otherwise we’d never get to the fun parts of physics).
Deriving escape velocity
Alright, now let’s work through the math.
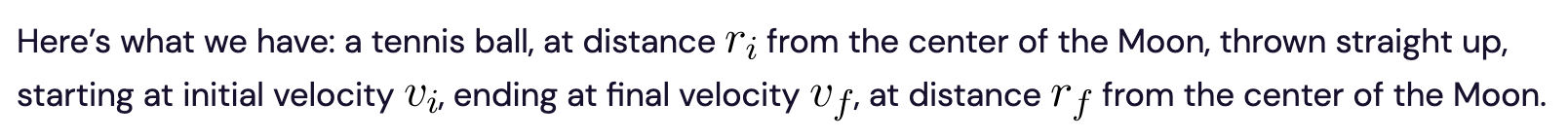
We can write our conservation of energy statement from the previous section as an equation, then write both terms in terms of our known variables.
We can write our conversation of energy statement from the previous section as an equation, then write both terms in terms of our known variables.
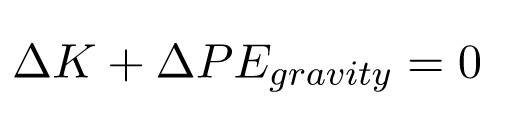
Let’s start with kinetic energy.
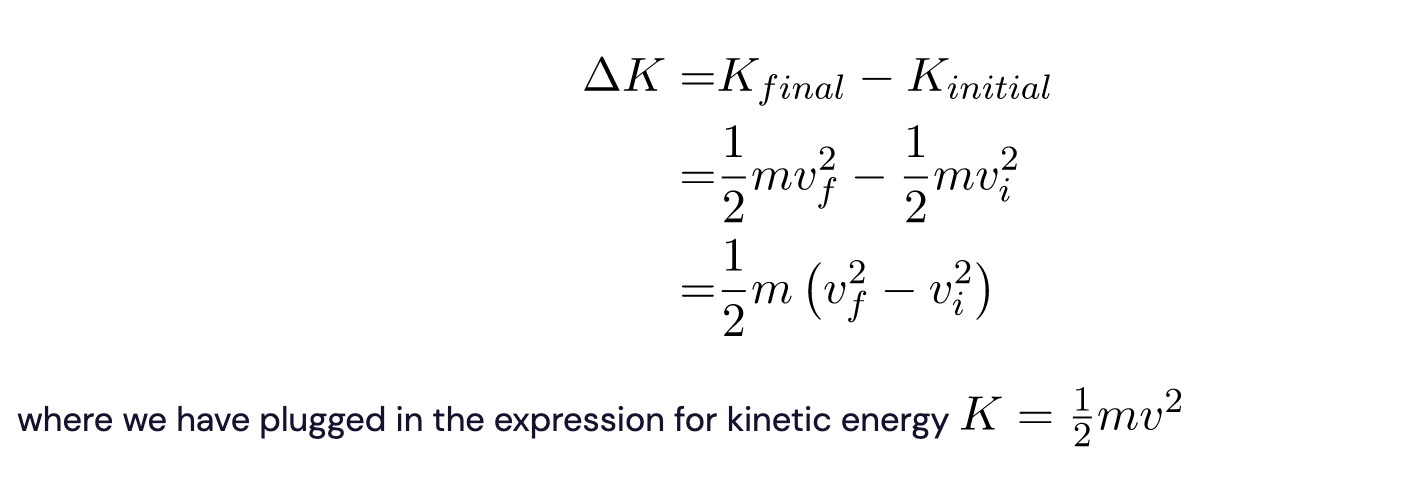
Now, let’s look at gravitational potential energy.
We can find the change in gravitational potential energy by integrating the gravitational force over the distance traveled by the tennis ball.
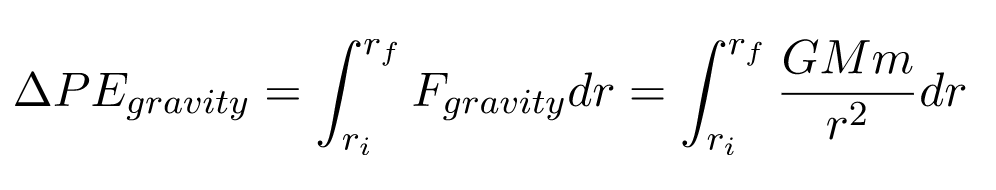
We can integrate this using the integral rules from single-variable calculus.
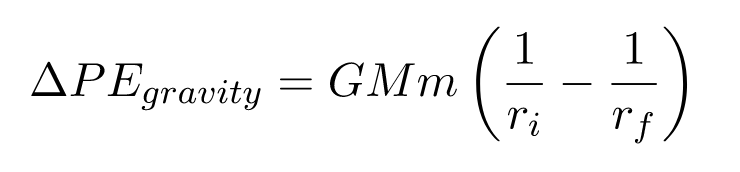
We want the potential energy needed for the tennis ball to reach infinity, so we set rf = infinity. Plugging this in gives us
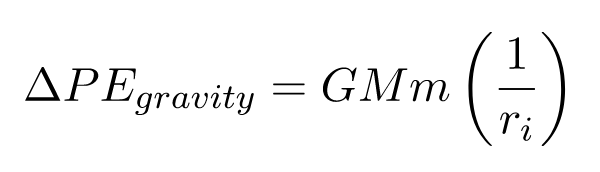
Plugging (2) and (3) into (1) gives us
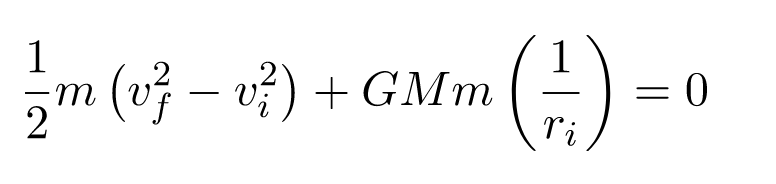

- We want to convert all the kinetic energy to gravitational potential energy
- If the final speed is greater than 0, that means there’s extra kinetic energy that we didn’t need to get all the way to infinity, which means we could have thrown the ball at a slower speed and still escaped the gravitational influence of the Moon.
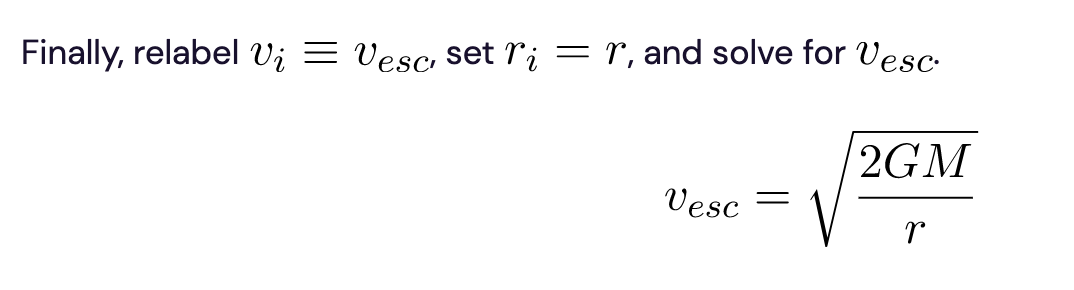 We’ve arrived at the equation for the escape velocity!
We’ve arrived at the equation for the escape velocity!
Some things this equation tells us:
- The ball’s escape velocity is given solely by the Moon’s mass and its initial distance from the Moon’s center. Nowhere did the object’s shape, composition, color, or any other feature come into play.
- The mass of the ball doesn’t matter! A ping-pong ball has the same escape velocity as a bowling ball.
- Mathematically, both the kinetic energy and the gravitational potential energy increase linearly with the ball’s mass, so changes in mass cancel out (look at Equation 4).
- Mathematically, both the kinetic energy and the gravitational potential energy increase linearly with the ball’s mass, so changes in mass cancel out (look at Equation 4).
- This is the escape velocity for any object; it doesn’t have to be a ball!
Some things this equation doesn’t tell us:
- How does the ball behave if it’s faster than the escape velocity? Where does all the energy go?
- How long would it take for a ball thrown at escape velocity to reach a given distance?
- Does direction you throw the ball matter? It turns out the value of the escape velocity doesn’t depend on the direction, but throwing a ball in any direction other than straight “up” will cause is to land in a different place or even enter into an orbit.
Is this how rockets work?
So have we just learned how rockets work? Not really. Here’s a few reasons why:
- Our escape velocity calculation assumed that gravity was the only force “pulling it down”. However, Earth’s atmosphere produces a drag that pushes back on the rocket.
- Our derivation for escape velocity assumed that once the ball was in the air, gravity was the only force acting on the object. In contrast, rocket engines fire during the entire ascent; the rocket is subject to both forces throughout.
- Spacecraft aren’t always trying to escape Earth. The energy needed to send a spacecraft to Mars is far more than that needed to have it reach Earth orbit.
Nonetheless, understanding escape velocity is an important first step in thinking through how objects in space behave and developing the skills to tackle rocket mechanics (if that’s what you’re super interested in!)
Like this post? Check out more posts by Max on his personal blog here.


Comments