Finding patterns in exponent problems on the GRE Quantitative section

One thing about GRE quant questions and standardized test math questions more broadly: if a question seems impossible or like it will take a ridiculously long amount of time to complete… It isn’t as difficult as it seems! Let’s dive right into a practice problem to see an example. Take the following numeric entry problem:

Let’s take a step back. So far, we have the following:

Notice anything? I think we may have a pattern of 7, 9, 3, 1, repeat. But let’s just calculate out another three digits to be sure.

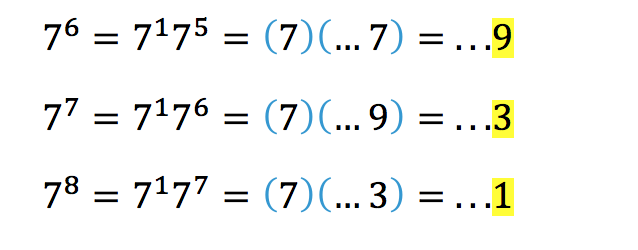
Yup, the pattern checks out! (Note: For future reference, units digit patterns for exponents come in cycles of at most four, so once you reach the fourth number you can stop and leverage the pattern you have found rather than wasting precious time on superfluous calculations. A caveat to this is that these patterns could also be LESS than four…)

So, how can this methodology be applied to different variations of GRE problems? As you can expect, the wording and style of the problems can vary considerably, but often the core approach taken to solve the question can be similar. Consider the following “select one or more answers” multiple choice question.

Now, before reading this post you may have wasted your time trying to carry out many calculations, hoping you got all the right digits. But, now that you are familiar with finding patterns in exponent cycles, this should be a breeze! n must be a positive integer, so let’s start with 1 and go from there.

Let’s try one more, this time a quantitative comparison question.

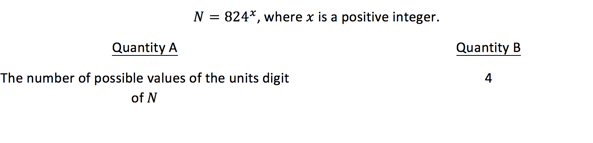
It looks like the pattern alternates between 6 and 4; it is 6, 4, repeat. Thus, there are only two possible values of the units digit for 𝑁. Meaning the value of Quantity A is 2. This means that Quantity B is greater, which is (B).

In conclusion: When you first see certain GRE quant problems, they can look completely foreign, or seem impossible. But with proper preparation, you can equip yourself with the key skills necessary to tackle those problems with ease. You can work your way through the different wordings and styles the test makers throw at you by leveraging a fairly low number of core competencies while also looking for patterns to find solutions more quickly.