I always tell my students not to be afraid to ask why. In so many parts of our lives, we are asked to defend our opinions and ideas—to offer evidence and to explain our thinking or reasoning. But sometimes, it feels this is missing from math education, especially in middle school and high school. Math becomes about memorizing formulas rather than about understanding how things work. So many times as students, we are told: “this works, it just does.” The thing is, that’s almost never the case. There are many types of explanations one might give: a formal proof, a derivation, enough data to extrapolate a pattern, or even just context for why something makes sense. But, to a question of, “why does this work?” very rarely should the answer be “it just does.”
In grade school math, perhaps few things are associated more with memorization than pi: there are competitions in many classrooms for who can memorize the most digits. When I first learned about pi, I was told it was the ratio between a circle’s circumference and diameter. I was told to accept that, and to memorize at least the first few digits. It did not even occur to me to wonder how we found that number.
In fact, there are many ways to approximate the value of pi that are accessible with math taught in traditional K-12 classrooms, and I want to share one with you.
Imagine inscribing a series of polygons inside a circle with radius 1. The more sides you add to your polygon, the closer you get to the circumference of your circle. Here, you can see a triangle (3 sides), square (4 sides), pentagon (5 sides) and hexagon (6 sides). We can imagine as we continue adding sides, our inscribed polygon will slowly start to look more and more like the circle.
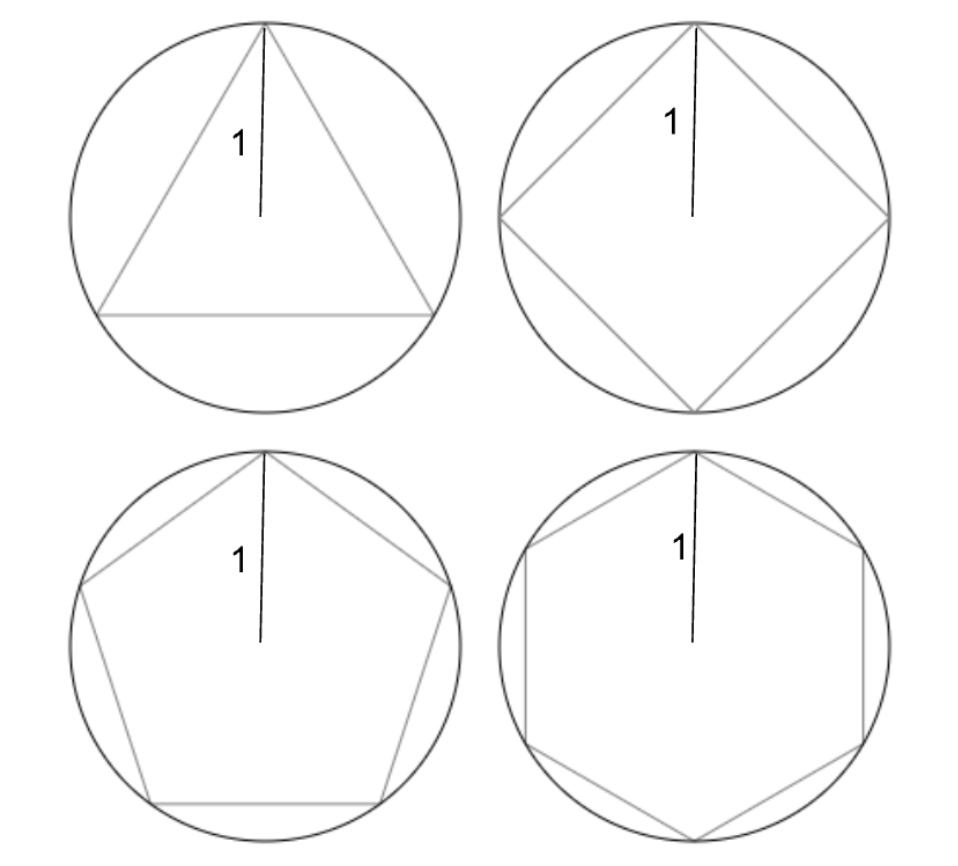
So, if we can find a pattern in the lengths of the perimeters of the polygons, we can use that pattern to estimate the circumference of the circle.
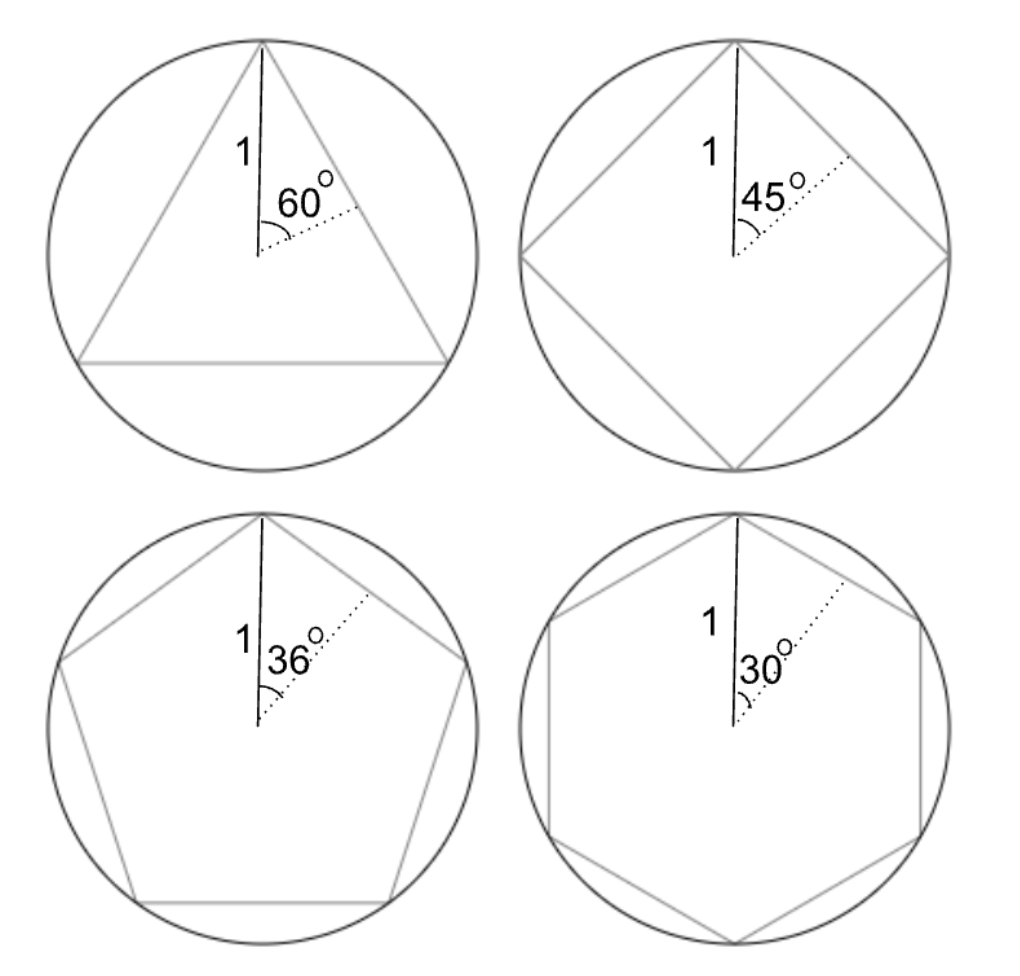
Let’s start by drawing a line from the center of our circle that is perpendicular to the side of each polygon. We have now created a right triangle within each polygon. Each has a hypotenuse of 1, and each has a different interior angle.
We can use sine to solve for the leg of the triangle that lies on the perimeter of each polygon. Let’s call those sides x.
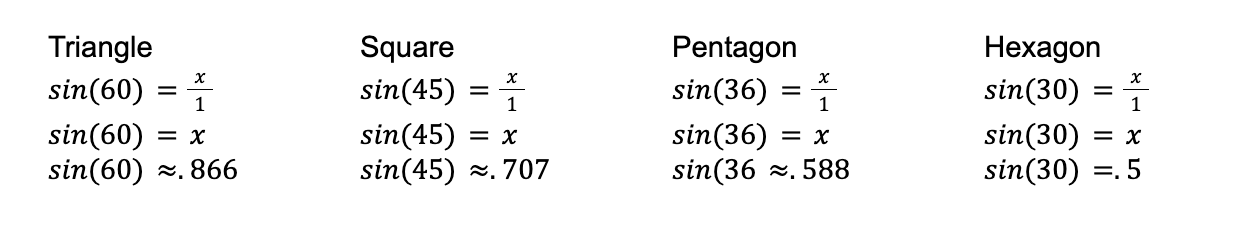
Now, let’s build each polygon’s perimeter out of those legs. There are 6 along the perimeter of the triangle, 8 along the perimeter of the square, 10 along the perimeter of the pentagon and 12 along the perimeter of the hexagon.
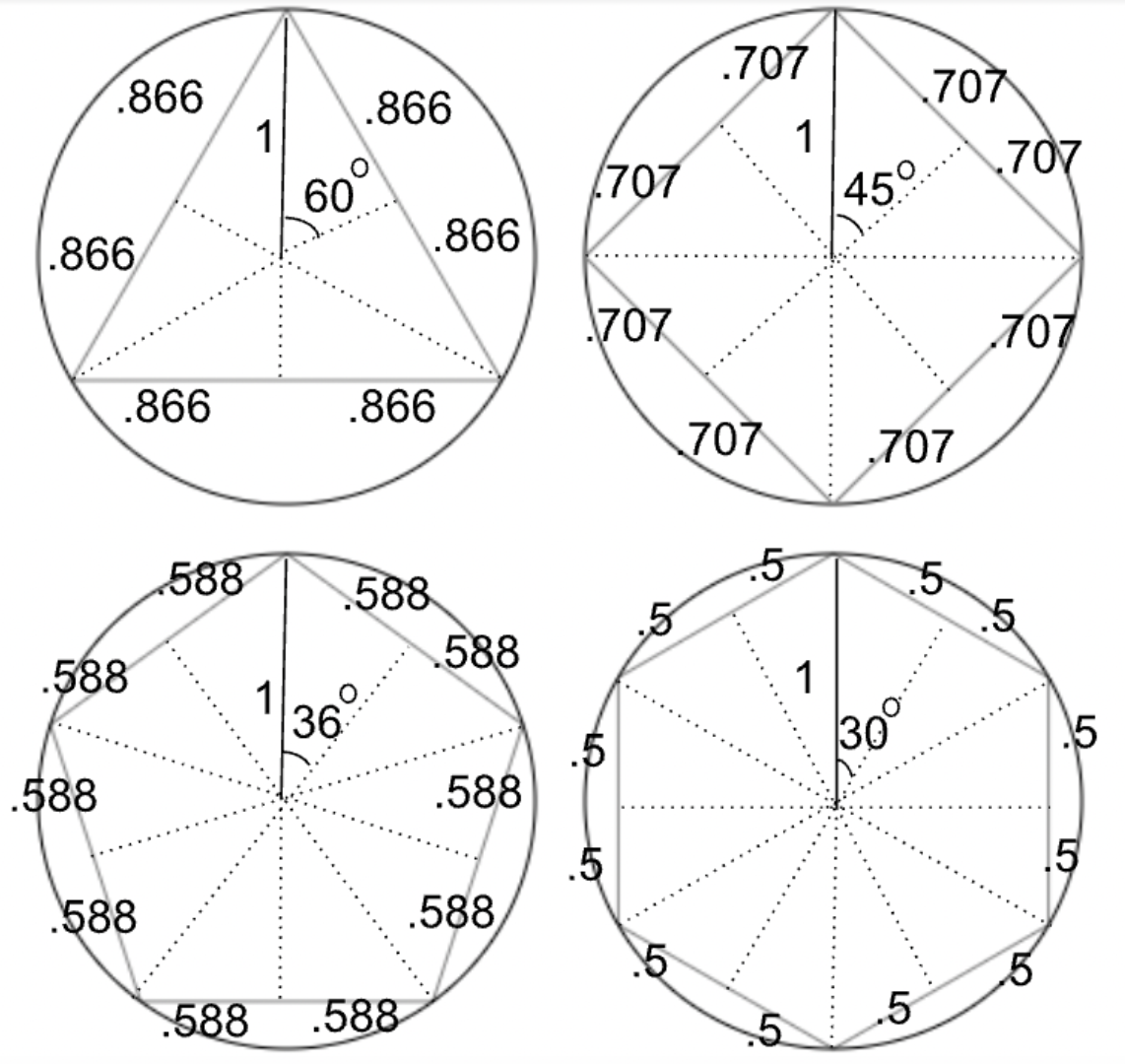
Our totals come out to:

Already, we can see a pattern emerging, but we are going to need to add a lot more sides to get anywhere close to a circle. Rather than repeating our method hundreds of times, let’s write a formula that does it for us. Let’s call the number of sides in our polygon n, and consider what we did in our first four cases.
In each case, we first created one right triangle with a different interior angle. That angle is simply 360/(2n). For a triangle, n=3, our angle was 360/(2*3) = 60. For a square, n=4, our angle was 360/(2*4) = 45, and so on.
Next, to find our legs, we simply took the sine of that angle, and multiplied by the hypotenuse which is 1 in every case. So, for a polygon of n sides, the leg we are looking for has a measure of sin(360/2n) units.
Lastly, we simply counted how many of those legs made up the perimeter of our polygons. In each case, the number of legs around the perimeter is twice the number of sides. For a triangle, there were 6, for a square 8, and so on.
This leaves us with our final formula. For a polygon with n sides, the perimeter is: sin(360/2n) * 2n.
Let’s try plugging in a large number, like 1000. (Feel free to plug in larger numbers if you’d like!)
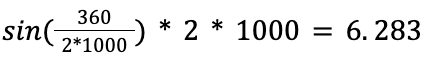
By this point, with 1000 sides, the perimeter of our polygon should be getting closer to the circumference of our circle. Now, our radius was 1 and that makes our diameter 2, so if pi is the ratio of the circumference to our diameter, then
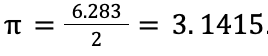
All circles are similar, so if this is the ratio for a circle of radius 1, it should be the ratio for all circles.
This explanation is based on Archimedes’ method of deriving pi, and can be made more formal. But even without calculus or anything beyond basic trigonometry, we no longer need to have faith in what someone else tells us: we can convince ourselves that pi–the ratio between a circle’s circumference and diameter–is approximately 3.14.
From trigonometric ratios, to the quadratic formula, to basic laws of exponents, to pi, there is always more to how something works than “it just does.” In my experience, not only is learning to ask why more productive than trying to memorize everything, it is more fun as well.


Comments