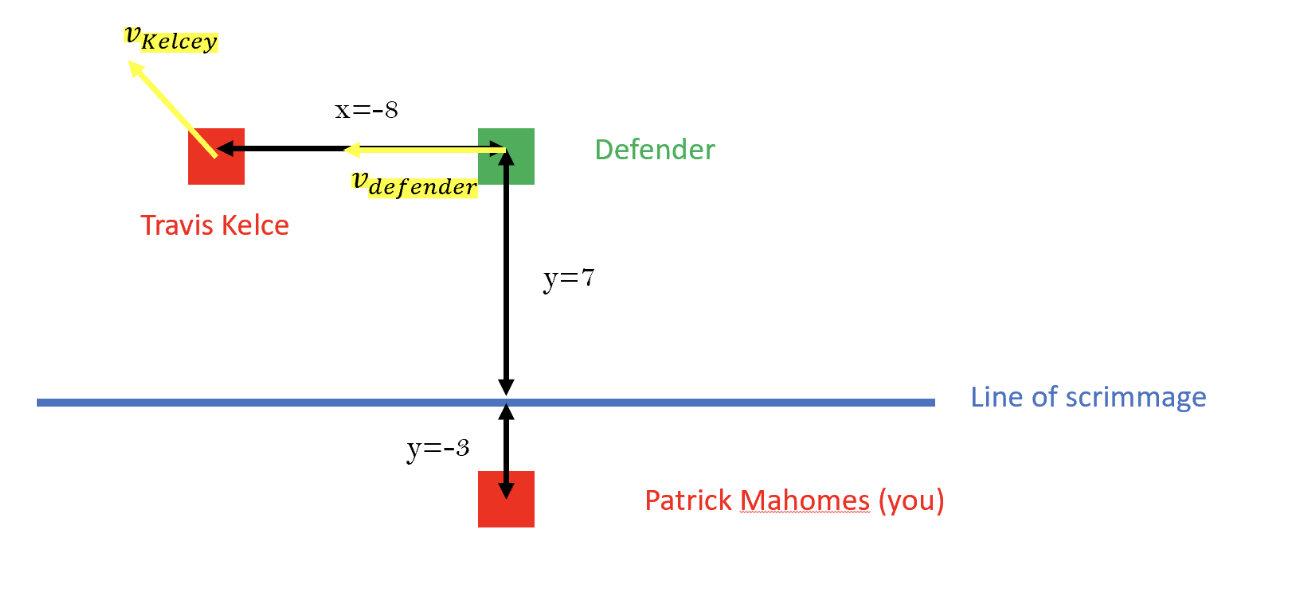
You are Patrick Mahomes, the quarter back for Kansas City in the National Football League. You are centered horizontally on the field and 3 meters behind the line of scrimmage with the ball in your hand, and you need to throw the ball to Travis Kelce, who is 7 meters ahead of the line of scrimmage and 8 meters to your left. Travis is running vertically up the field (away from you) at 5 meters per second and horizontally away from a defender (and away from you) at 6 meters per second.
If you want the ball to reach Kelce by meeting him at 10 meters to your left, with what velocity do you need to throw the ball to for the ball to reach Kelce? Assume no acceleration from Kelce.
If a defender is as far down the field as Kelce (y=7 meters) and running at Kelce at 8 meters per second horizontally and 5 meters per second vertically from the same horizontal position as you (x=0 meters), how much time do you have before the defender reaches Kelce (assuming no acceleration)? Will you get the ball to him before the defender gets there?
Consider our known variables.
We know the velocity (or combination of horizontal and vertical speeds) of Kelce, 𝑣𝑥𝐾𝑒𝑙𝑐𝑒 = −6 𝑚/𝑠, 𝑣𝑦𝐾𝑒𝑙𝑐𝑒 = 5 𝑚/𝑠. We know the velocity of the defender, 𝑣𝑦𝑑ef𝑒𝑛𝑑𝑒𝑟 = 5 𝑚/𝑠, 𝑣𝑥𝑑𝑒𝑓𝑒𝑛𝑑𝑒𝑟 = −8 𝑚/𝑠. We know the starting location of Kelce, 𝑥𝐾𝑒𝑙𝑐𝑒 = −8 𝑚, 𝑦𝐾𝑒𝑙𝑐𝑒 = 7 𝑚. We also know the starting locations of the defender and ourselves, 𝑥𝑑𝑒𝑓𝑒𝑛𝑑𝑒𝑟 = 0 𝑚, 𝑦𝑑𝑒𝑓𝑒𝑛𝑑𝑒𝑟 = 7 𝑚, 𝑥𝑀𝑎ℎ𝑜𝑚𝑒𝑠 = 0 𝑚, 𝑦𝑀𝑎ℎ𝑜𝑚𝑒𝑠 = −3 𝑚. And lastly, we know the final horizontal position that we want the ball to reach Kelce, 𝑥𝑓𝑖𝑛𝑎𝑙 = −10 𝑚. Notice that we have oriented our coordinate system to be centered at the center on the line of scrimmage, as opposed to be centered where we are throwing from.
It's time to solve the problems.
Let's define our unknown value, set up the equations, solve them, and plug in values.
We want to know the velocity we need to throw the ball to reach Kelce at 10 meters to your left. That velocity will be composed of the horizontal speed, 𝑣𝑥𝑏𝑎𝑙𝑙, and vertical speed, 𝑣𝑦𝑏𝑎𝑙𝑙. To calculate the speeds (distance divided by time), we will need to know the initial and final positions of the ball, as well as how much time the ball has to travel the distance between those initial and final points. We already know the initial horizontal and vertical positions and the final horizontal position, so we will need to figure out the time for travel and the final vertical position.
So, let’s find the time, 𝑡𝑓𝑖𝑛𝑎𝑙, before Kelce reaches 10 meters to your left, or 𝑥𝑓𝑖𝑛𝑎𝑙 = −10 𝑚𝑒𝑡𝑒𝑟𝑠, from his position, 𝑥𝐾𝑒𝑙𝑐𝑒.
Let's set up the equation for speed:
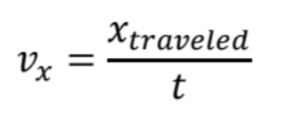 Now, arrange for our desired variable, 𝑡𝑓𝑖𝑛𝑎𝑙, and plug in the values:
Now, arrange for our desired variable, 𝑡𝑓𝑖𝑛𝑎𝑙, and plug in the values:
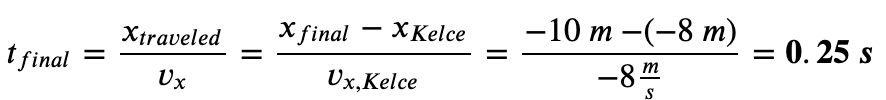
Next, we need to know Kelce’s final vertical location, 𝑦𝑓𝑖𝑛𝑎𝑙. Set up our equation of motion, knowing Kelce’s starting position is 𝑦𝐾𝑒𝑙𝑐𝑒 and vertical speed 𝑣𝑦𝐾𝑒𝑙𝑐𝑒:
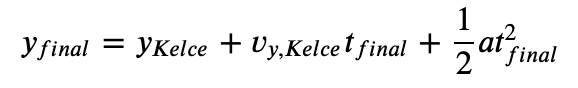 In our case, we are assuming no acceleration, so 𝑎 = 0. No algebra is needed as this equation is already setup for our desired variable:
In our case, we are assuming no acceleration, so 𝑎 = 0. No algebra is needed as this equation is already setup for our desired variable:
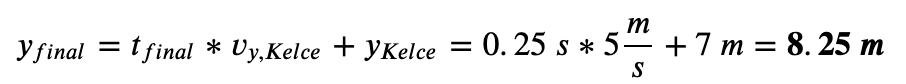
Now we know Travis’s final position, 𝑥𝑓𝑖𝑛𝑎𝑙, 𝑦𝑓𝑖𝑛𝑎𝑙 and the time to get there from our known position, so let’s find the velocity we need to throw the ball with by calculating the horizontal and vertical speeds (𝑣𝑥,𝑏𝑎𝑙𝑙, 𝑣𝑦,𝑏𝑎𝑙𝑙) needed to reach those points within time, 𝑡𝑓𝑖𝑛𝑎𝑙. Recall that we are throwing from behind the line of scrimmage, which is what we used as our coordinate system to designate the position to which we will throw the ball.
Let's set up our equations for velocity:

Now we'll plug in our values:
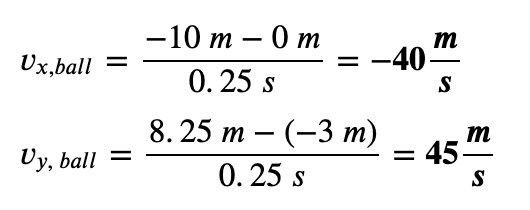
The ball velocity will be -40 m/s in x and 45 m/s in y.
Finally, consider how much time we have before the defender reaches Kelce. Let’s call that time 𝑡𝑑𝑒𝑓𝑒𝑛𝑑𝑒𝑟. Recall that Kelce and the defender are at the same position vertically and are moving at the same speed vertically, so we just need to consider the difference between their horizontal speeds to calculate how long until they meet.
Let's use the equation for speed and arrange for our desired variable, 𝑡𝑑𝑒𝑓𝑒𝑛𝑑𝑒𝑟:
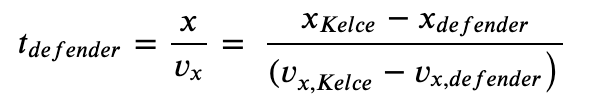
Now, let's plug in our values. Recall that we have our coordinate system set so that moving left is moving in the negative x direction.
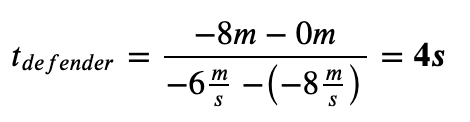
Kelce will get the ball before the defender gets to him! Yay!


Comments