All you’ll need for this project is a computer that can run Python, 30 hours of free time, and an 18-foot aperture parabolic antenna.
How can hydrogen help us peer into the structure of the universe? In hydrogen, the interaction between the nucleus and the electron creates two possible states for the electron spin. The proton and electron can either be aligned in the same direction, or in opposite directions. These two states have different energy levels, and hydrogen atoms can transition between these states. This is known as “hyperfine splitting”. When hydrogen atoms switch between these states, they emit a photon (a particle of light) with a wavelength of 21 centimeters. You may have heard of “21 centimeter radiation” - that’s exactly what this is!
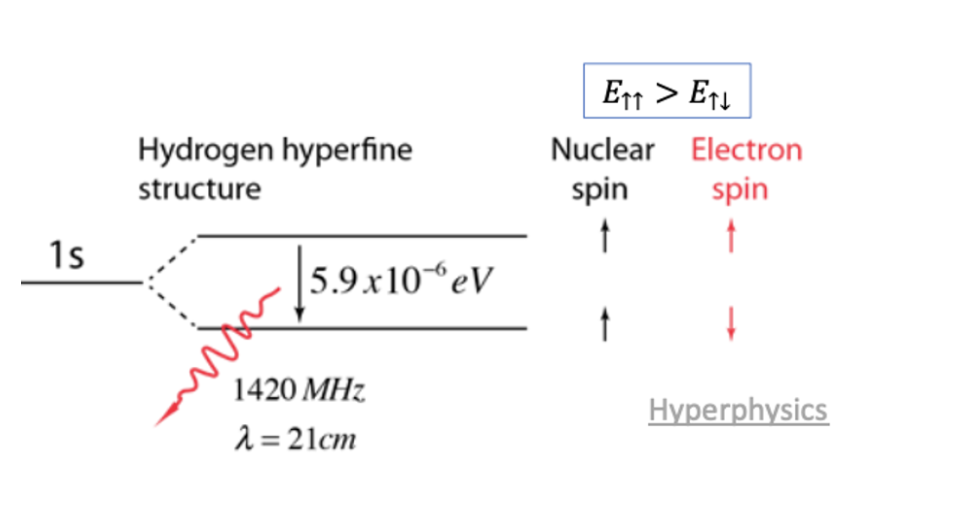
A wavelength of 21 centimeters falls into the radio wave region, so a radio telescope can pick up this radiation. This was all predicted in 1944 by van de Hulst, and was observed in 1951 at Harvard, and many other institutions.
What can we learn with 21cm data? It will tell us about the rotation curve of the galaxy. The rotation curve describes how fast a point moving at a certain distance away from the center of the galaxy is moving. It characterizes the shape and behavior of a spiral arm galaxy, and different galaxies have different rotation curves. The rotation curve will even let us deduce the structure of the Milky Way!
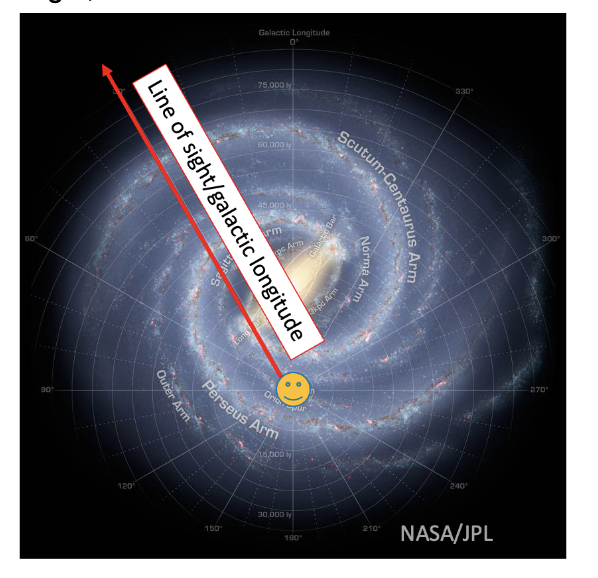
 By looking at clouds of hydrogen gas in the universe, we can observe the 21cm radiation. I used the Big Radome telescope at MIT to scan the sky. We scan the universe by looking along different lines of galactic longitude, which means different lines of sight. This is measured as an angle, l.
By looking at clouds of hydrogen gas in the universe, we can observe the 21cm radiation. I used the Big Radome telescope at MIT to scan the sky. We scan the universe by looking along different lines of galactic longitude, which means different lines of sight. This is measured as an angle, l.
 In circular motion, the relationship between the tangential velocity (velocity in a line) and rotational velocity (velocity around a circle) is given by v = rw. Since we’re rotating around the center of the galaxy, we have to take into account our motion relative to the galactic center. We have to subtract out our rotational motion so we can calculate the rotation curve of the entire galaxy.
In circular motion, the relationship between the tangential velocity (velocity in a line) and rotational velocity (velocity around a circle) is given by v = rw. Since we’re rotating around the center of the galaxy, we have to take into account our motion relative to the galactic center. We have to subtract out our rotational motion so we can calculate the rotation curve of the entire galaxy.
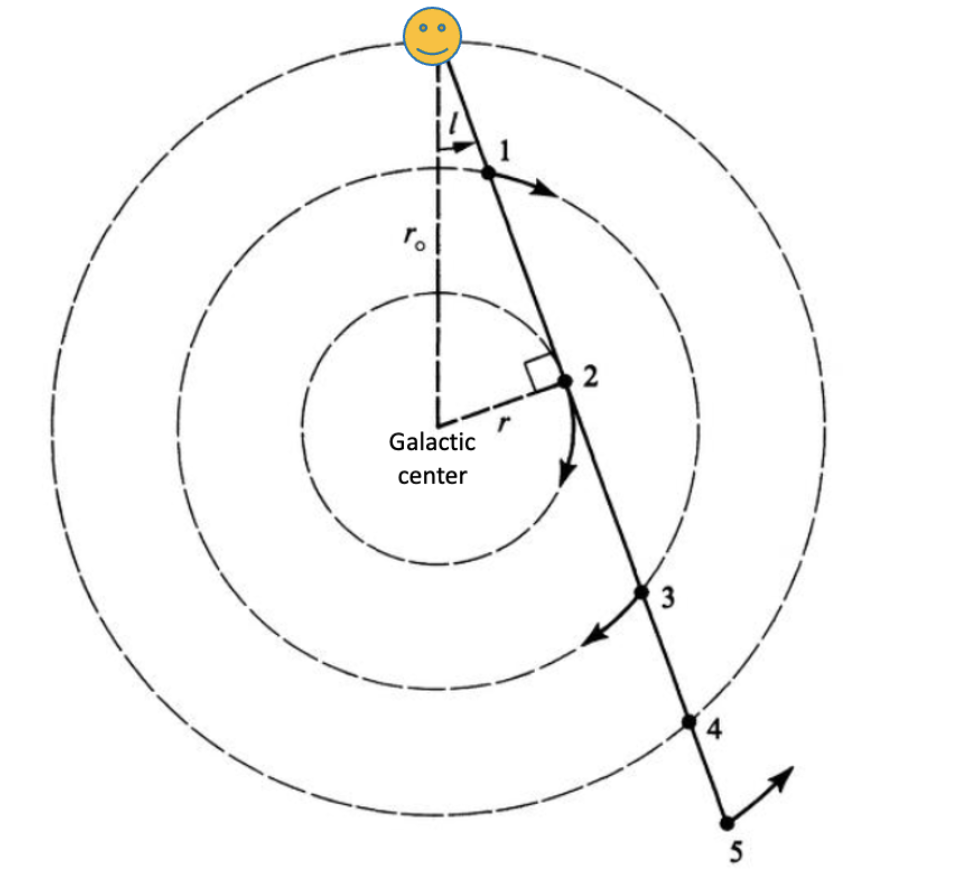

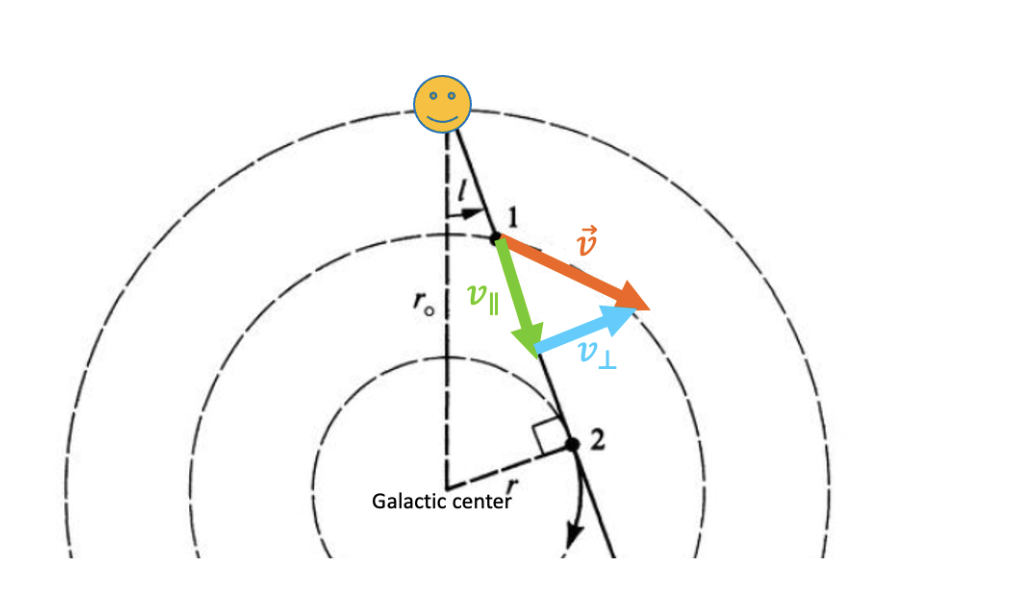
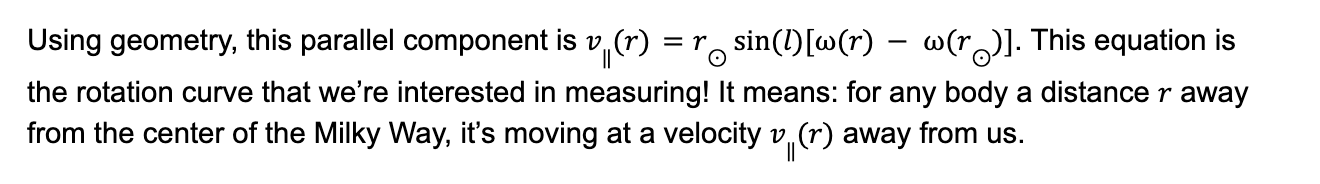
Now that we’ve theoretically calculated what we’re trying to measure, let’s measure it (as we know, all good physics requires experimental verification). But there’s one problem: how do we measure only one component of a velocity? Well, look at point 2 on the diagram above, and notice that at point 2, all of the velocity is parallel to the line of sight! So if we measure the speed of the radiation at point 2 for many lines of sight, we can measure the rotation curve!
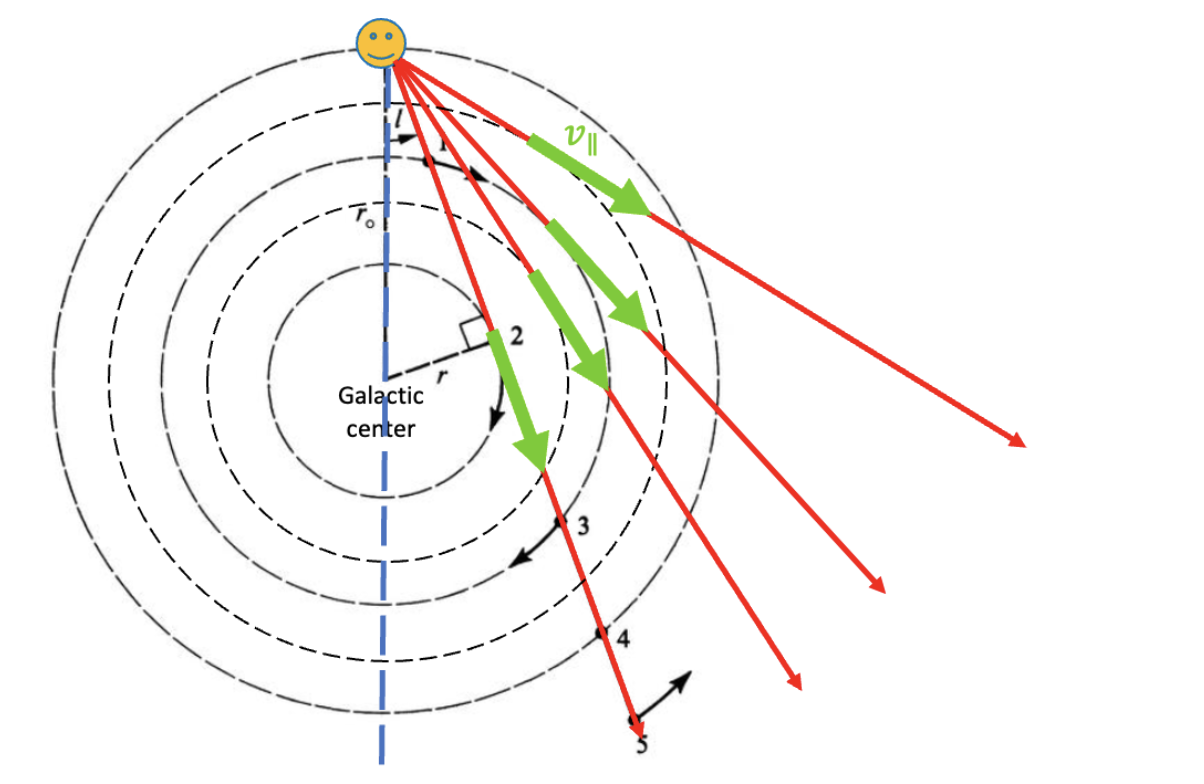
It’s important to note that since the hydrogen gas at point 2 is moving directly away from us, it will be the most Doppler-shifted data. So I measured the velocities of 21cm radiation against the intensity of that radiation.
The right-most point is the most Doppler-shifted hydrogen gas, which corresponds to the gas at points like point 2 in the diagram above. For these points, marked in red in the graph, I stored the velocities of each of these points, for many galactic longitudes.

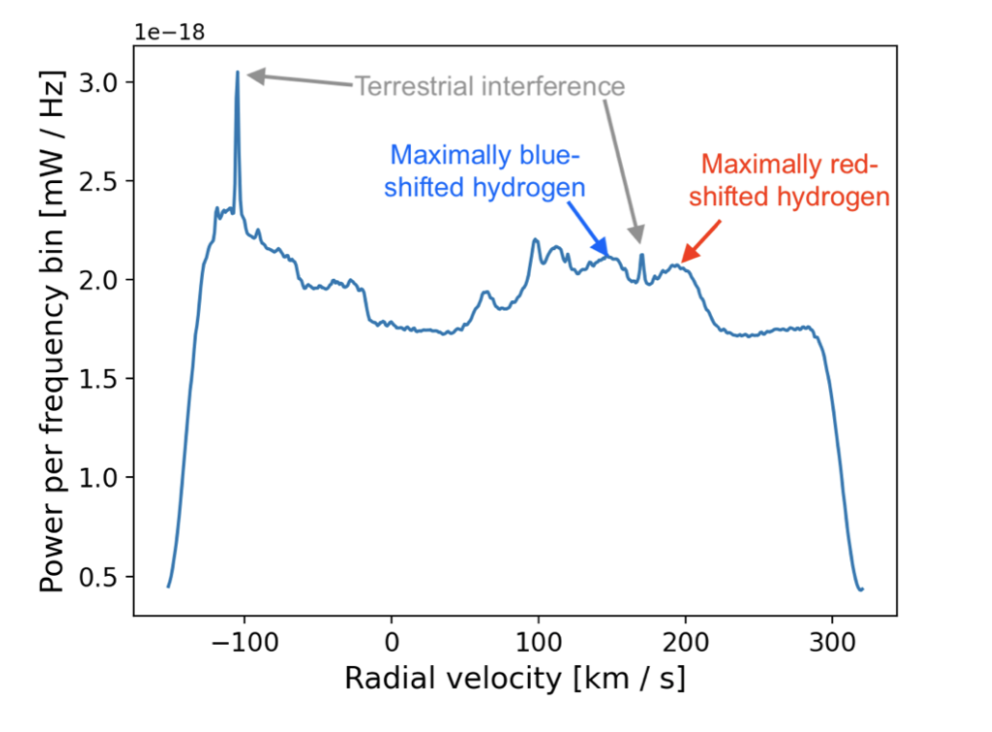
So, I plotted the velocity (which I got from the graph above) versus r, which is exactly the rotation curve!
You’ll notice that the data falls sharply around ~2-3 kpc from the center. Why’s that? Well, at that point, 21cm data becomes unreliable, because there’s a huge black hole at the center of the galaxy!
This plot, combined with the intensity profiles of the hydrogen gas, tells us where the “stuff” in our galaxy is. So, if I use polar coordinate representation with r versus l (the galactic longitude), I can plot where all the “stuff” in the galaxy is:
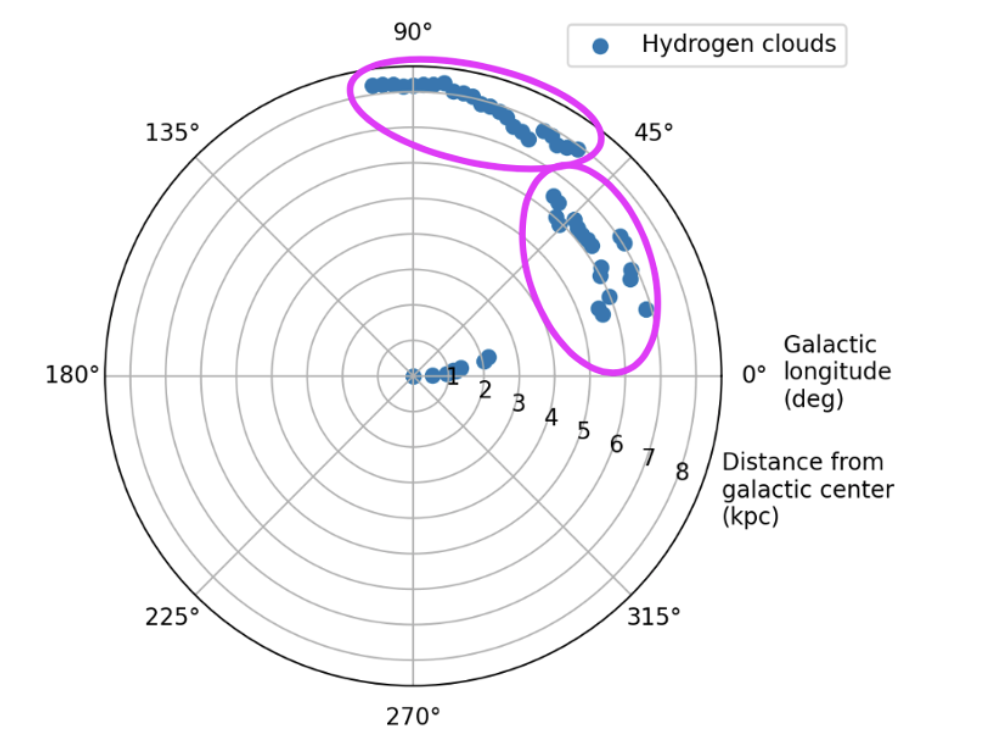
Let’s compare this to some verified data. Below is a comparison of my plot with a NASA/JPL artist rendering of real data:
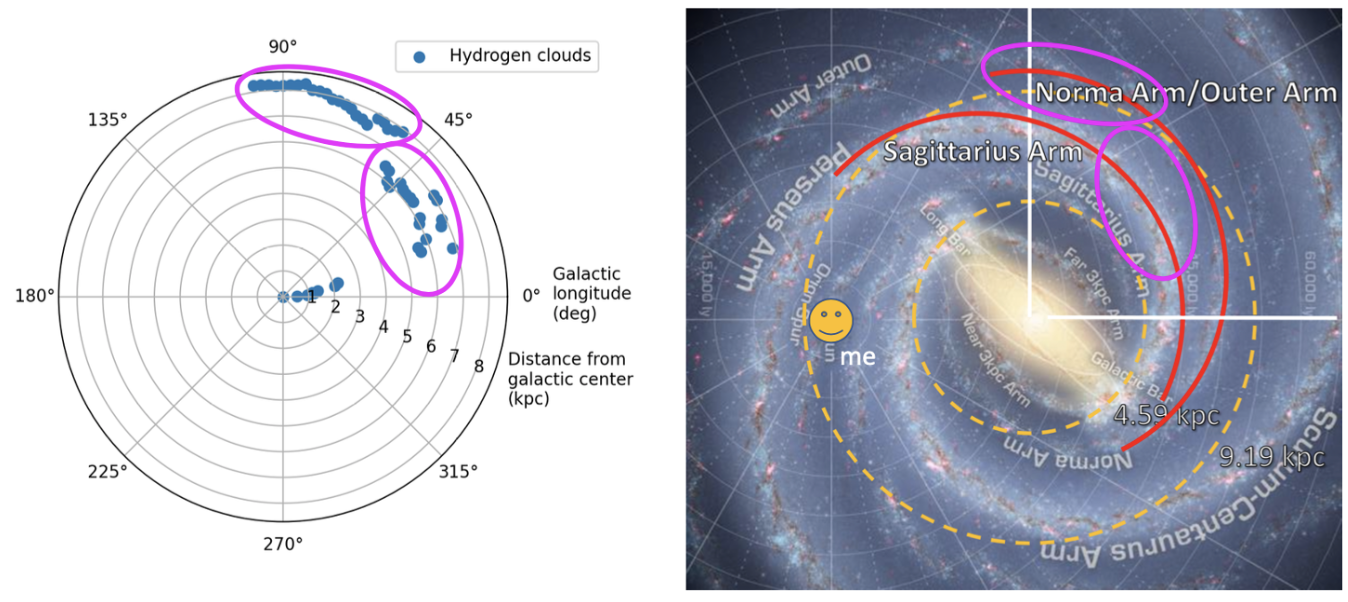
Looks like I might’ve captured the Saggitarus Arm and the Norma Arm of the Milky Way!!
How would I see the other parts of the galaxy? Actually, we can’t see a lot of the Milky Way! The black hole in the center of the galaxy causes some problems with measurements, and we’d need REALLY big telescopes (on the order of the diameter of the Earth). But a lot of the radiation from the other side of the Milky Way is actually scattered or absorbed along the way to our telescopes.
We could use gravitational measurements, since they don’t depend on electromagnetic radiation. But we’re just getting started using gravity for observational astrophysics. Typically, we use observations of other galaxies (e.g. Andromeda) to make assumptions about the structure of our own.
So, if you ever wanted to know the structure of the stars just by using your knowledge of rotational physics, geometry, and a giant radio telescope, that’s how you’d do it!


Comments