How to prove the Pythagorean Theorem

The Pythagorean Theorem plays an essential role in many facets of math from Euclidean Geometry to complex numbers to trigonometry. Today we’ll explore one of its many proofs.

We normally think about the Pythagorean Theorem as a description of the relationship between lengths (specifically in a right triangle), but what if, instead of lengths, we thought about it as a description of the relationship between areas?

Let’s start with the following figure:

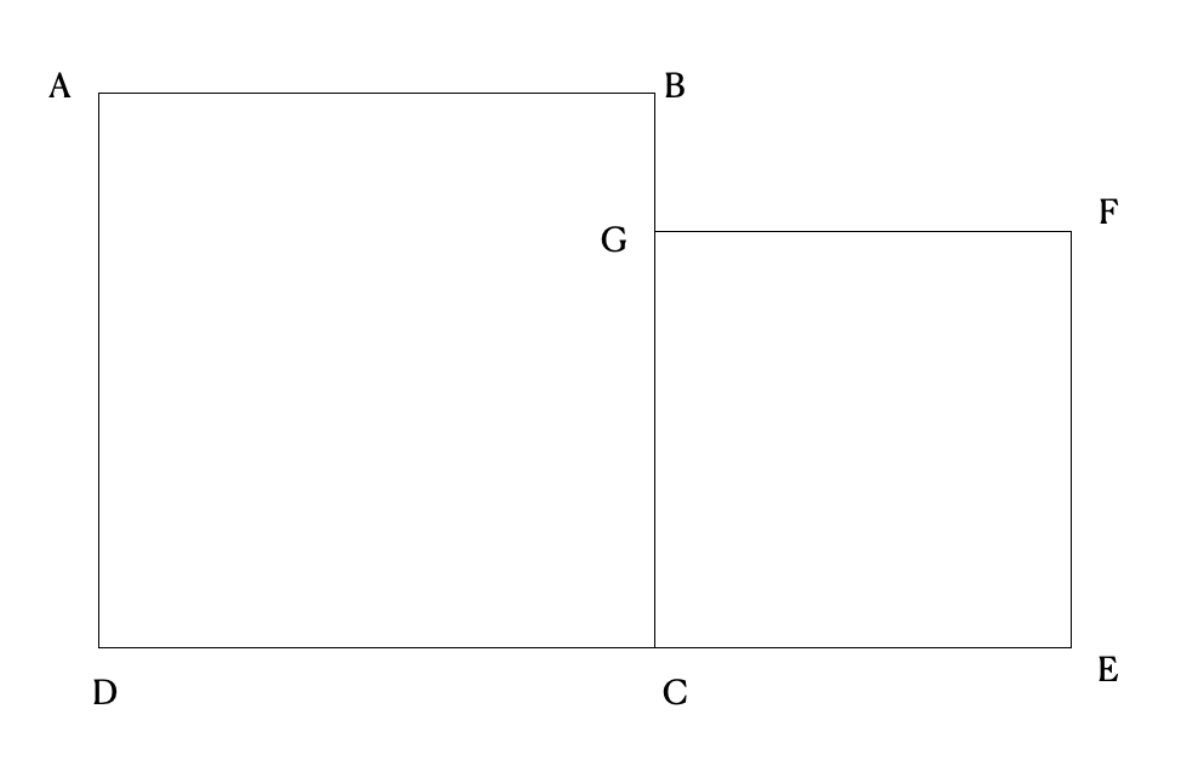Here we have two squares placed side by side. Our goal will be to cut these squares up into pieces and rearrange the pieces such that they form a new, larger square. If we can do this, we will have created a new square with an area equal to the sum of the areas of the two original squares. (Hopefully this should ring a bell and relate back to the Pythagorean theorem).

First try this on your own, and if you’re still stuck after a few minutes, read on!

Proving Congruency

Our first step will be to add a point (let’s call it P) to DC such that DP=CE. Now let’s create line segments AP and PF. What do we know about these two segments? Why?

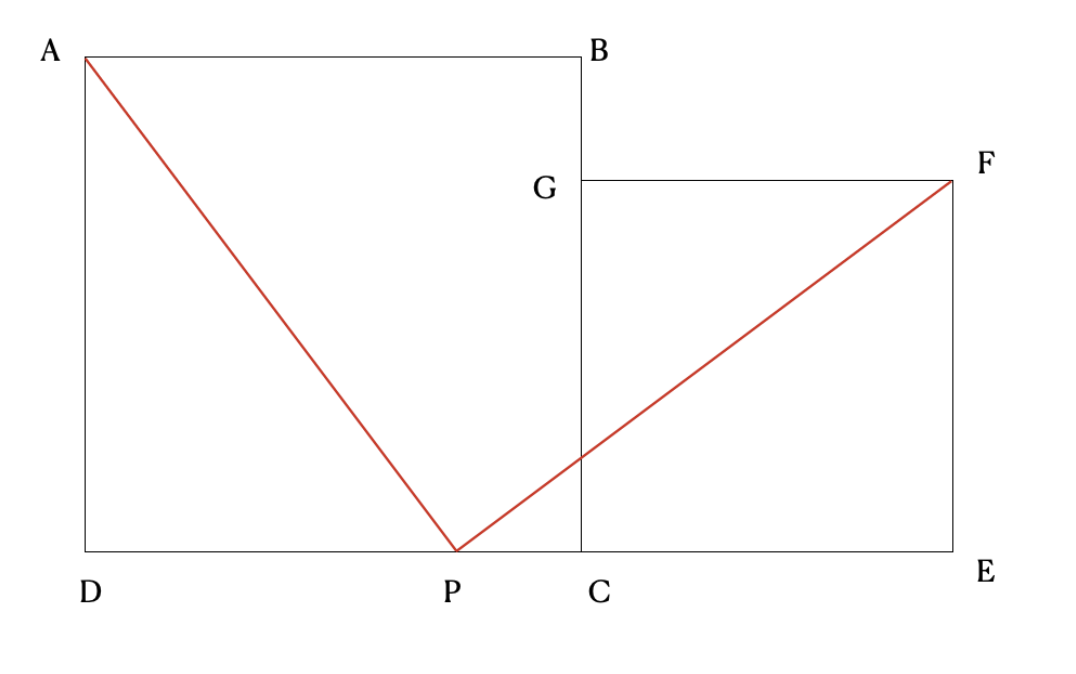
It turns out that AP and PF are congruent! To justify this, let’s look at triangles ADP and FEP. If we can show that the triangles are congruent, then we will have proven that AP and PF are congruent.

We chose point P such that DP=CE. Because GFEC is a square, CE=FE. Thus, by the transitive property, DP=FE. 

We also know that DE=DC+CE and DE=DP+PE. Because DP=CE, we can replace DP with CE in the prior equation to give us DE=CE+PE. From this it follows that DE-CE=PE and DE-CE=DC. Again, by the transitive property, PE=DC. Because ABCD is a square, PE=AD. 

Angles ADP and FEC are both right angles, so they are congruent, thus by SAS, ADP and FEP are congruent. 

If you’re confused at this point, go back and give the two squares actual dimensions (say CE=3 and DC=4), and try to come to the same conclusion about AP and PF; then come back and work your way through the generalized proof. Or, take a look at this color coded figure, and see if it helps.

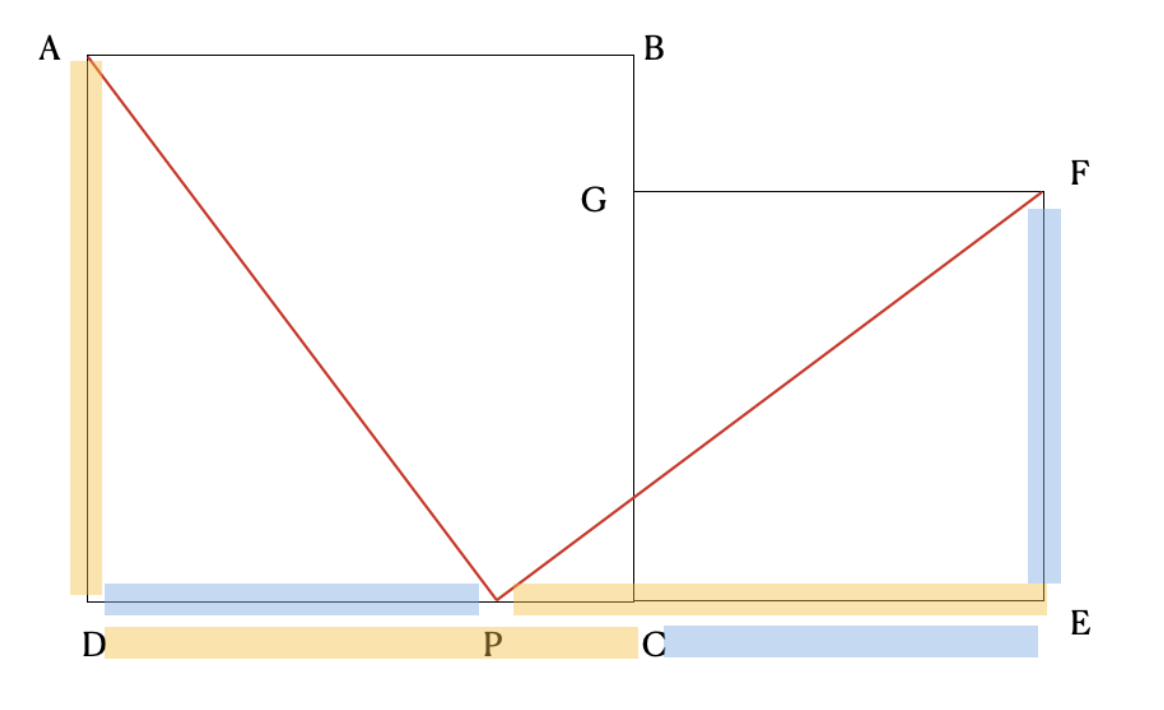
Creating the square

Look at the figure again… did you notice that AP creates the hypotenuse of a triangle with side lengths equivalent to the side lengths of our two original squares? We’ll store this information in our back pocket for now and continue our original task: cutting up these squares to form a new square.

First we’ll remove triangle PFE, rotate it 90 degrees clockwise and move it upwards so that FE aligns with GF. Here’s what it will look like:

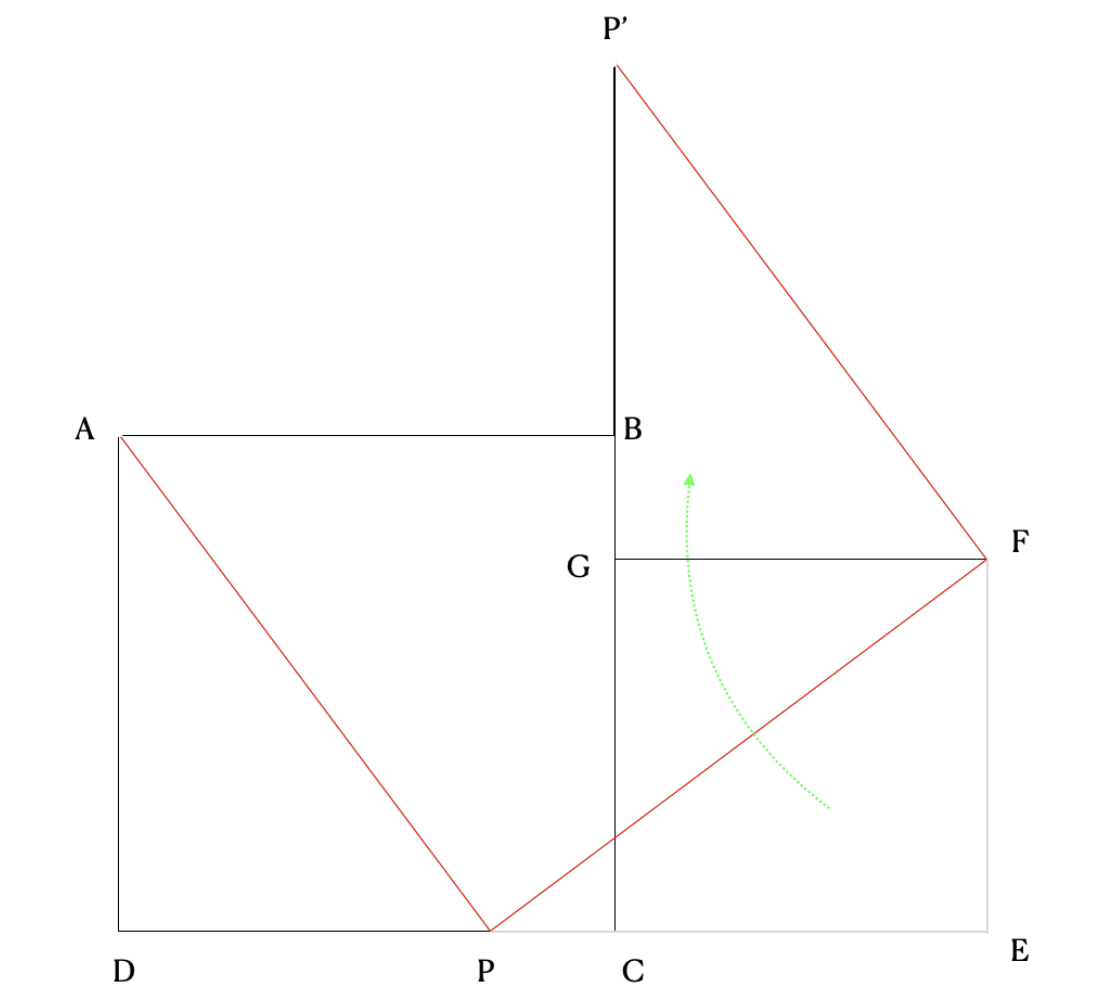
We will manipulate triangle ADP similarly so that AD lines up with AB:

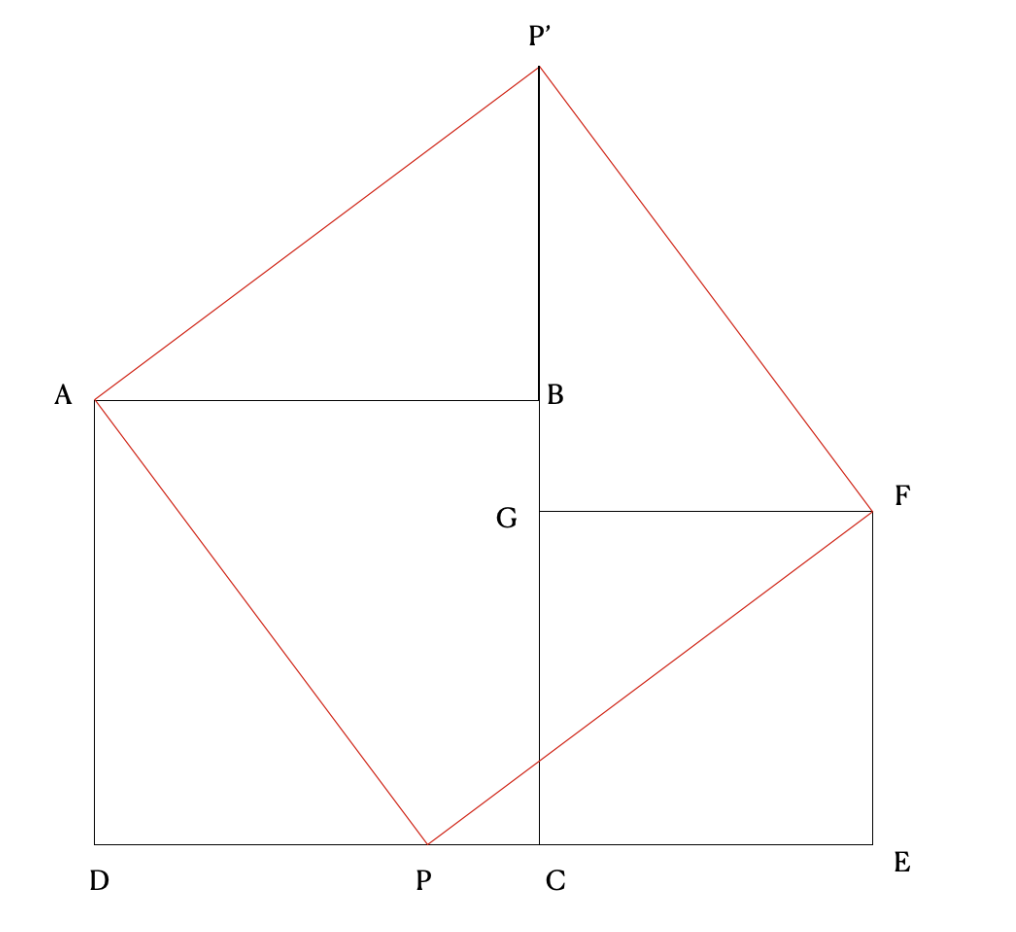Proving the theorem

We have now created a new shape (in red) whose area is the sum of our two original squares AND its side length is the hypotenuse of a right triangle with the other sides congruent to the sides of the two original squares.

What do we have left to show to complete our proof? See if you can finish the proof on your own!

To prove the Pythagorean theorem with finality, we need to show that when we rotate and translate the triangles, they do indeed create a square. We will first need to show that P’ is the same point for both FGP’ and P’BA. In other words, we need to show that our rotate and translated triangles do indeed meet at one point. 

Mathematically, this means showing that the image of P’B+BG= the image of GB ie, DP+BG=PE

We’ll start by manipulating BG, expressing it as differences of other segments, and replacing these with segments we have previously shown to be congruent to get:

BG=BC-GC=DC-CE=DC-DP=PC

Going back to our original two squares, we have

DP+PC=DC

Thus DP+BG=DC, and therefore: DP+BG=PE

When we rotate ADP and stack DP onto BG, we then know that DG will be congruent to the rotated segment PE, which gets stacked onto GF. Therefore, our two rotated triangles will intersect in the same point P’

We have now shown that there exists a quadrilateral PAP’F, and our prior work (in the proving congruency section) tells us that this quadrilateral has four congruent sides. To prove that it is a square, we need to show that it has one right angle.

Because there are 180 degrees in a triangle and ADP is right in D by construction, angles DAP and APD must add to 90 degrees. Because triangles ADP and PEF are congruent (as previously shown), angles DAP and EPF are congruent. Thus angles APD and FPE must add to 90, and therefore the measure of angle APF must be 90 degrees because APD, APF, and FPE are supplementary.

Therefore, AP’FP is a square and its area is the sum of the areas of ABCD and GFEC. 

From this, it follows that AD²+CE²=AP² and so AD²+DP²=AP²

For any right triangle, the sum of the squares of the two shorter sides will equal the square of the hypotenuse.