If you’re majoring in economics, you will likely also need to take a statistics course. One of the trickiest concepts is dealing with conditional probabilities. In most classes, they teach you a fairly complicated equation known as Bayes’ Theorem.
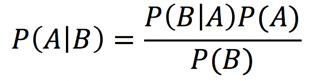
While this isn’t a hard formula to plug values into, it doesn’t give an intuitive understanding of what the conditional probability P(A|B) actually is. Also, think about being a few years out of school – what are the chances you’ll remember Bayes’ Theorem and properly calculate a conditional probability?
One of my professors taught a more visual method to evaluate conditional probabilities, known as probability trees. When you’re confronted with a question about the probability of one event dependent on another event, just remember to draw a tree!
Here’s an example problem that shows how to apply this method. Suppose someone is getting tested for Tuberculosis (TB). TB is relatively rare these days, so let’s say only 1% of the population has the disease. Also, the test for the disease is 99% accurate. This means that if you have TB, there is a 99% probability you will have a positive test, and if you do not have TB then there is a 99% probability you will have a negative test. How likely is a patient to have TB if he gets a positive test result? To solve this problem, put the given information into a probability tree. 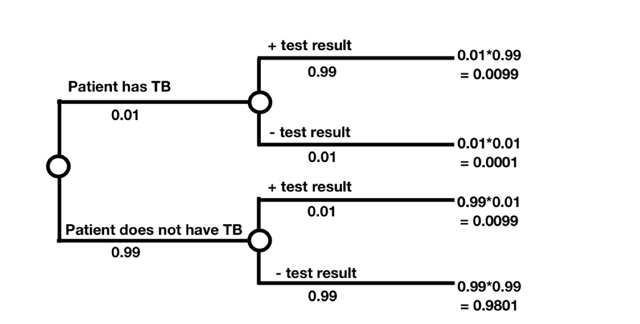
The information about the test accuracy is a conditional probability. If you have TB, there is a 99% probability that you will have a positive test result; if you do not have TB, there is a 1% chance you will have a positive test result. The sum of probabilities on each set of branches from a node should be one. If the probability someone has TB is 1%, we know the probability someone does not have TB is 99%.
Now, we have to calculate the intersection probabilities. These are the probabilities that a patient has TB and has a given test result or that a patient does not have TB and has a given test result. To calculate the intersection probabilities, which are shown at the terminus of each branch, multiply all of the probabilities along a specific branch. The calculations are shown in the tree diagram.
Notice that we have the probability of a positive test result given disease status, but we actually want to know the probability of having TB given a positive test result. To answer how likely a patient is to have TB given a positive test result, we need to “flip” the tree. To flip the tree, redraw the tree and place the events in the correct order along the branches. The intersection probabilities will be the same, so the probabilities at the end of the branches will still be the same for each pairing of events. The unconditional probability of a positive test result is the sum of the probability a patient has TB and has a positive test result and the probability that a patient does not have TB and has a negative test result. Similarly, the unconditional probability of a negative test result is the sum of the probability a patient has TB and has a negative test result and the probability a patient does not have TB and has a negative test result.
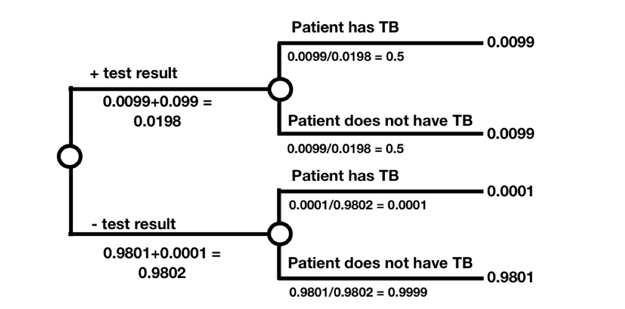
The final probability to calculate is the conditional probabilities, which are along the second set of branches. Recall that to get the intersection probabilities, we multiplied along the unconditional probability and the conditional probability along each branch. Therefore, we divide the intersection probability by the unconditional probability to get the probability a patient has a disease conditional on the test result. Finally, we see that P(Patient has TB | positive test result) is 50%.
Bayes’ Theorem would give us the same answer as the probability tree flip.Feel free to use whichever method you find more intuitive. Often professors present only one of these methods, and it can be helpful to see the solution to a problem with a different technique.


Comments