 Imagine that you and a friend are going to the movies. You like comedies more than action movies, while your friend likes action movies a lot more than comedies. If you go to see a movie alone, however, you’re probably not going to have as much fun, regardless of what type of movie you see. What is the optimal behavior for each person in this situation? At first glance, it seems hard to know exactly what will happen, since the payoff or reward that you receive will depend not only on which movie you go see but also what movie your friend decides to see.
Imagine that you and a friend are going to the movies. You like comedies more than action movies, while your friend likes action movies a lot more than comedies. If you go to see a movie alone, however, you’re probably not going to have as much fun, regardless of what type of movie you see. What is the optimal behavior for each person in this situation? At first glance, it seems hard to know exactly what will happen, since the payoff or reward that you receive will depend not only on which movie you go see but also what movie your friend decides to see.
What is game theory?
In economics, we can model this situation as a game with players, actions they can take, and payoffs that they receive in different situations. A key aspect of game theory is that the payoffs to one player depend on the decision that they make and on the decision that other players make. This means that in order for individuals to maximize their own payoffs, they must consider and predict what the other player(s) in the game will do as well. This is different from many of the simpler models in economics, where individuals’ payoffs from decisions they make are not affected by the decisions of other people (e.g. buying a sweater or a pair of shoes).
We can model the game as follows: first, the players in the game are simply you and your friend, because each of your decisions affect one another. Next, we can think of all the possible actions in of the players - either you can see a Comedy or an Action movie, and your friend has the same two choices. Lastly, we can write the payoffs for each player depending on what actions are chosen. In this case, these are just numbers that represent how valuable different outcomes are for each player.
Table 1 is the model of this game written out. It shows the players (“You” and “Your Friend”), their possible choices (see a “Comedy” or “Action” movie), and the payoffs to each player based on the actions that are chosen (the cells in the table, with numbers in parentheses). The payoffs are displayed so that the first number is the payoff to you, while the second number is the payoff to your friend. For example, a payoff of ( 4, 3 ) indicates that your payoff is 4 while your friend’s payoff is 3.
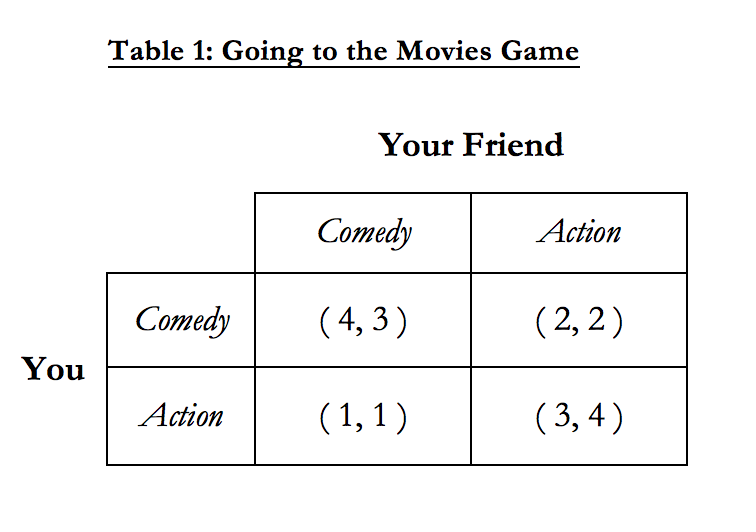
Using Table 1, we can see how different combinations of actions lead to different payoffs for each player. For example, if you both choose “Comedy”, then the payoff is ( 4, 3 ) as mentioned earlier, while if you both choose “Action” instead, the payoff would be ( 3, 4 ), which is better for your friend (a payoff of 4 vs. 3) but worse for you (a payoff of 3 vs. 4). This represents the fact that you like comedies better than action movies and your friend prefers action movies to comedies.
We can also see that when you choose “Comedy” and your friend chooses “Action” the payoff is ( 2, 2 ). In this case, you both get to see your favorite type of movie, but since both of you are going to different movies, the payoffs are lower. Similarly, if you choose “Action” and your friend chooses “Comedy”, then the payoff is only ( 1, 1 ), since neither of you get to see your favorite movie type and you’re watching the movie without each other - the worst of both worlds!
How can we use game theory to figure out the optimal decisions?
In order to predict how you and your friend will act, we need to find the Nash Equilibrium - a scenario (or scenarios) where nobody wants to change their behavior given the behavior of the other players. Nash Equilibrium is an important concept in game theory because it helps predict people’s behavior, even in complicated situations where one person’s payoff depends on another person’s actions. First, let’s use Table 1 above to figure out the optimal behavior for “You”, considering all possible actions of “Your Friend”
No matter what your friend does, you only have two possible actions: to see a Comedy movie or to see an Action movie. What should you choose? Well, it depends on what your friend is doing! Let’s consider the case where your friend is going to see a Comedy (focus on the first payoff in parentheses, and the “Comedy” column in Table 1). Either you can see a Comedy with them - and get a payoff of 4 - or you can go see an Action movie without them - and only get a payoff of 1. So, if your friend chooses Comedy, then you definitely want to go see a Comedy with them. What if your friend is seeing an Action movie instead (now the first payoffs for the “Action” column in Table 1)? Now, if you choose Comedy you only get a payoff of 2, while if you choose Action you’ll get a payoff of 3. In this second case, you’ll choose to see an Action movie with your friend rather than a Comedy by yourself. In other words, your optimal behavior is to always choose to see the same type of movie as your friend, regardless of what type of movie it is. We know this is true because that strategy always leads to the highest payoff for you, as an individual.
Now we need to consider the actions of your friend, given that we’ve figured out the optimal strategy for you. If your friend is choosing to see Comedy, and you are following the optimal strategy of watching Comedy with them, should your friend change their decision and watch an Action movie instead (their favorite type of movie)? If they stick with watching a Comedy with you, their payoff is 3, while if they switch to Action their payoff would only be 2 - so they stick to Comedy in order to maximize their own payoff.
But wait - this means we’ve found a Nash Equilibrium! When both you and your friend are choosing to watch a Comedy together, neither of you wants to change and watch an Action movie alone. In other words, nobody wants to change their behavior given the behavior of the other player. This is the definition of a Nash Equilibrium, so we can say that both players choosing Comedy is a Nash Equilibrium.
What if, instead, your friend is originally choosing Action? We know that you’ll want to choose Action as well since that’s your optimal strategy. Again, we can see that if you’re both choosing Action, neither you nor your friend will want to change your behavior and see a Comedy alone (even though you like comedies more than action movies!). This means that both players choosing Action is another Nash Equilibrium. Table 2 below shows the two Nash Equilibria and the payoffs in bold:
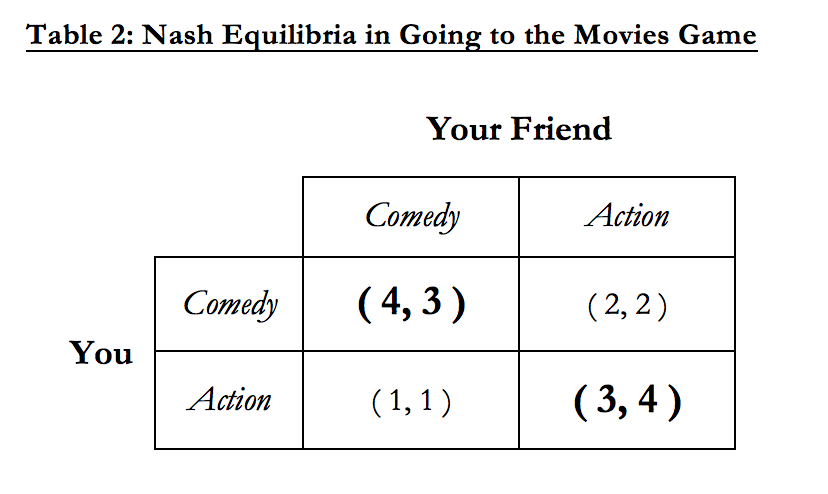
So, what will be the ultimate result of this “game” with your friend? What type of movie will you both end up seeing (what decision do you both end up choosing)? Because there are two Nash Equilibria in this game, we can’t predict exactly what will happen - there are two plausible outcomes (the two Nash Equilibria). We may not know whether you’ll both see a Comedy together or instead both see an Action movie together, but we can be sure that neither of you will choose to watch a movie alone. That’s because, like we showed before, the optimal strategies for both you and for your friend are to choose to watch whatever movie the other person is watching, and never watch a different movie alone. This game structure is a common example of a coordination game, a game where the Nash Equilibria are situations where both players need to coordinate to choose the same course of action in order to maximize their payoffs. Not all games have multiple Nash Equilibria - some of them only have one, and some more complicated games have more than two! But finding the Nash Equilibrium (or the Nash Equilibria) is an essential part of game theory which helps economists think about and predict human behavior in complicated scenarios.

Comments