Motivating matrices: why do we care about linear maps?

If you’re reading this, you probably already know what a matrix is. But just to be clear, a matrix is a rectangular array of numbers. Here is an example:

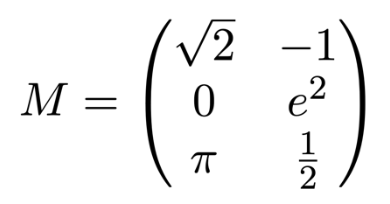
This matrix, which we are calling “M”, has 3 rows and 2 columns, so we say that it is a 3×2 (“three by two”) matrix. The number π is in the third row, first column, so we say that the (3,1) entry of M is π. Matrix entries are often written as lowercase letters with subscripts, so we may say m_3,1 = π, and m_1,2 = -1.

Matrices (and higher-dimensional arrays, called tensors) are a great way to organize many types of data, but in the context of linear algebra they have a more specific purpose. A matrix represents a linear map.

What is a Linear Map?

A linear map is a type of function between vector spaces. For now, don’t worry about the general definition of a vector space. We will stick to some basic examples here: the (one-dimensional) real number line, the (two-dimensional) Cartesian plane, and three-dimensional coordinate space. Points in these spaces are called vectors. They can be added together (by summing each coordinate) and scaled by real numbers.

A linear map is a function which preserves the operations of addition and scalar multiplication:

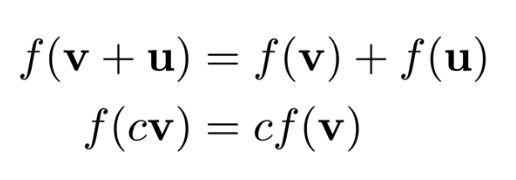
The name comes from the geometric fact that the graph of such a function is a flat passing through the origin (a one-dimensional flat is a line).

How a Matrix Represents a Linear Map

To completely determine a linear map, it suffices to know what the map does to the unit coordinate vectors. For a map from n-dimensional space to m-dimensional space, there are n coordinate directions in the domain, and output vectors have m coordinates, so the map is specified by m*n numbers. These numbers are arranged in an m×n matrix.

Our 3×2 example matrix above represents a linear map from the two-dimensional Cartesian plane to three-dimensional space. The vector (1,0) in the plane is mapped to the vector (square root of 2,0,π), while the vector (0,1) is mapped to (-1,e²,1/2). To determine the image of any other vector, we can use these values and the properties of linear maps. For a general vector (x,y):

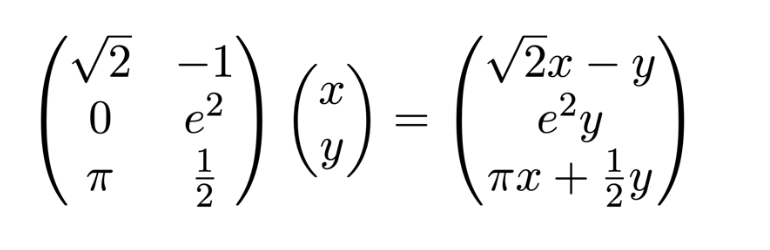
Here we are following the standard convention of writing vectors as n×1 matrices. The action of a linear map on a vector is then a specific case of matrix multiplication.

Why We Care About Linear Maps

Perhaps you are coming into linear algebra having recently studied calculus. In calculus, we see a wide range of different functions, most of which are not linear. And when it comes to functions of a single variable, linear maps are painfully simple: lines through the origin determined by a single value, slope. In higher dimensions, it is still true that almost all functions are not linear. So, why should we focus on linear maps when there is such a vast world of functions out there?

Among all functions, linear maps are some of the simplest. Even if you were skeptical of my claim that simplicity can be painful, surely you will agree that too much complexity can feel bad too. In higher dimensions, there is no shortage of complexity, and the simplicity of linear maps is cherished. Can you gain satisfying understanding from studying exotic non-linear higher dimensional functions? Of course. But linear algebra is already a very rich subject, and since the objects of study are simpler, you can develop greater understanding more quickly.

Many ideas in geometry and mathematics at large can be expressed in terms of linear maps, and many real-world relationships are linear too. But we can apply our understanding of linear maps to a much broader class of functions. Just as slope gives rise to a (first order) approximation for a single variable function, higher-dimensional derivatives produce linear maps which approximate the local behavior of multivariate functions. This allows us to apply insights from the simpler case directly to more complex problems.

Lastly, the algebraic structures generated by linear maps via matrix multiplication have found applications far beyond their original geometric interpretation. There is a rigorous sense in which they are some of the most general examples of continuous algebraic groups. To study matrix algebra is to gain understanding of continuous symmetries and transformations at large.