Given the recent rise of big data, there continues to be growing interest in the field of data science. One of the most basic, yet most useful tools for a data scientist is the linear regression model. Let's walk through the basics behind simple linear regression—a statistical model used to study the relationship between two variables.
Definition & Terminology
In basic terms, simple linear regression is a modeling technique that enables us to summarize the trend between two variables. The adjective “simple” is not meant to demean linear regression models—it’s a reference to the fact that simple linear regression only involves the analysis of two variables. One variable, often referred to as the predictor, explanatory, or independent variable, is denoted x. The other variable, commonly known as the response, outcome, or dependent variable, is denoted y. These terms are interchangeable; however, their use varies across different fields of study. You should note that there are also “multiple” linear regression models that involve the analysis of multiple predictor variables; however, we will not cover that topic in this blog post.
The easiest way to describe a simple linear regression model is using graphical terms. Suppose that we have a standard Cartesian graph plotted with several (xi,yi ) data points. In building a simple linear regression model, we seek to determine the “best fitting line”—the most appropriate line through the data. The equation for this best fitting line is defined as follows:
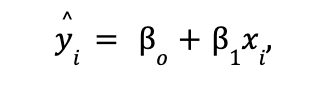 where xi denotes the observed predictor value for experimental unit i, yi denotes the observed response value for experimental unit i, ^yi is the predicted response or “fitted” value for experimental unit i, and Bo and B1 are the coefficients of the best fitting line. More specifically, o represents the y-intercept of the best fitting line and 1 represents the slope of the best fitting line. Also note that an “experimental unit” is simply the object or person on which the specific measurement is made.
where xi denotes the observed predictor value for experimental unit i, yi denotes the observed response value for experimental unit i, ^yi is the predicted response or “fitted” value for experimental unit i, and Bo and B1 are the coefficients of the best fitting line. More specifically, o represents the y-intercept of the best fitting line and 1 represents the slope of the best fitting line. Also note that an “experimental unit” is simply the object or person on which the specific measurement is made.
Remember that a best fitting line leads us to a predicted response value, yi , and predictions are not always entirely accurate. This leads to “prediction error” (also known as “residual error”) defined as follows for each experimental unit i:
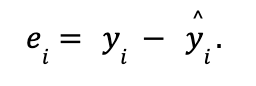 The line of best fit will be the one for which the n prediction errors (where n represents the total number of experimental units or data points) are as small as possible in some overall sense. For example, the “least squares criterion” is a common approach, which says that the regression coefficients Bo and B1 that define the best fitting line are those that minimize the sum of the squared prediction errors. It can be difficult to solve for these coefficients by hand, yet luckily most programming languages such as R will do it for us!
The line of best fit will be the one for which the n prediction errors (where n represents the total number of experimental units or data points) are as small as possible in some overall sense. For example, the “least squares criterion” is a common approach, which says that the regression coefficients Bo and B1 that define the best fitting line are those that minimize the sum of the squared prediction errors. It can be difficult to solve for these coefficients by hand, yet luckily most programming languages such as R will do it for us!
Example—Iris Dataset
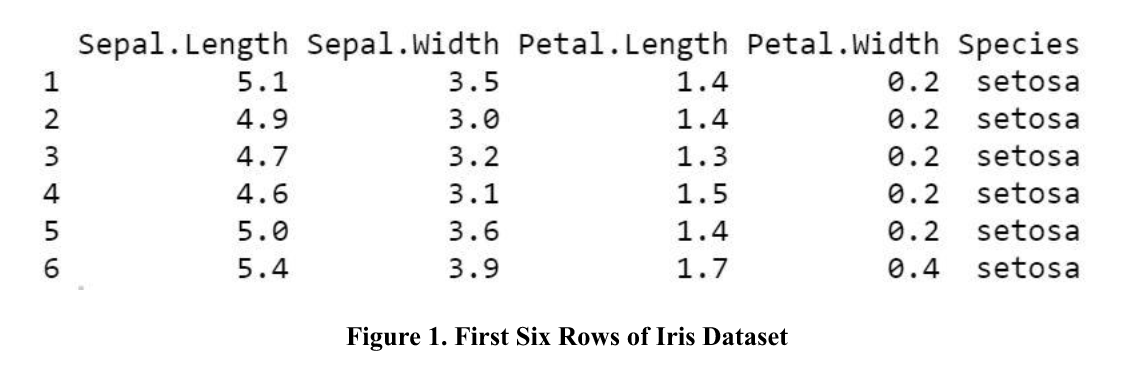
Any student interested in studying data science should be exposed at some point to the Iris dataset—it’s a built-in dataset in R that contains measurements (in centimeters) on four attributes (i.e., sepal length, sepal width, petal length, and petal width) for fifty flowers from three different species. Figure 1 included below displays the first six rows of this dataset.
Graphing the petal length (cm) versus the petal width (cm) of all 150 experimental units included in the dataset results in the scatterplot shown below as Figure 2. Note that this plot includes the best fitting line, which you may recall can be obtained by finding the Bo and B1 coefficients that minimize the sum of the 150 squared prediction errors. The equation of this line of best fit is defined as ^yi = 1.08+2.23xi, where ^yi represents the predicted petal length of experimental unit i and xi represents the observed petal width of experimental unit i. Note that all R code used to produce these two figures is included in Appendix A.
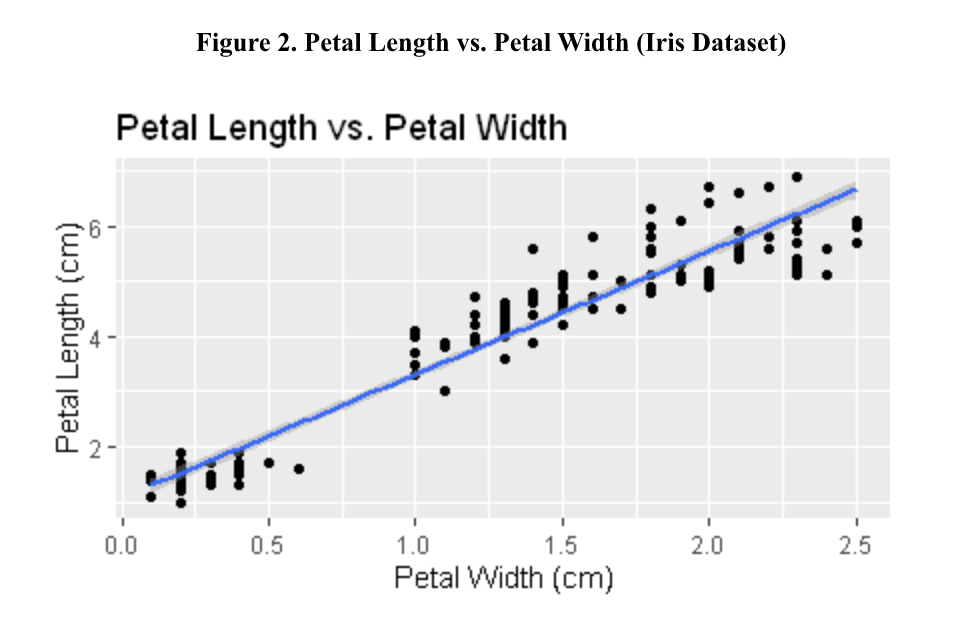 The plot included above as Figure 2 provides us with several useful insights. Based off this plot, there appears to be a positive linear association between the petal length and the petal width of Iris flowers (i.e., as the width of a flower’s petal increases, its length increases as well). Using the coefficients from the line of best fit, we can make even more precise inferences. The intercept coefficient, Bo, tells us that if the petal width of an Iris flower is 0 cm, then we’d expect its’ petal length to be approximately 1.08 cm. Note that in some instances this coefficient does not prove to be very meaningful, such as this one since it would be impractical for the petal width of a flower to be 0 cm. The slope coefficient, B1, tells us that every 1 cm increase in an Iris flower’s petal width is associated with an approximately 2.23 cm increase in petal length on average.
The plot included above as Figure 2 provides us with several useful insights. Based off this plot, there appears to be a positive linear association between the petal length and the petal width of Iris flowers (i.e., as the width of a flower’s petal increases, its length increases as well). Using the coefficients from the line of best fit, we can make even more precise inferences. The intercept coefficient, Bo, tells us that if the petal width of an Iris flower is 0 cm, then we’d expect its’ petal length to be approximately 1.08 cm. Note that in some instances this coefficient does not prove to be very meaningful, such as this one since it would be impractical for the petal width of a flower to be 0 cm. The slope coefficient, B1, tells us that every 1 cm increase in an Iris flower’s petal width is associated with an approximately 2.23 cm increase in petal length on average.
Beyond the inferences made in the previous paragraph, we can also use the line of best fit to make predictions. For example, suppose that we have an Iris flower whose petal width is 1.75 cm. Using the equation of our best fitting line, we’d expect the petal length of this flower to be ^yi = 1.08+2.231.75=4.9825 cm. There will likely be some error in this prediction; however, we can use the equation of the best fitting line to obtain a reasonable prediction of the petal length of any Iris flower, given just its petal width. Note that this value should ideally lie somewhere within the range of the observed petal widths included in the dataset, as this results in a more reliable prediction (this concept is known as “interpolation”).
Conclusion
Ultimately, this blog post provides a basic level introduction to the concept of simple linear regression. However, it should not serve as an all-inclusive guide, as there are several topics associated with regression modeling that are not covered in this post (e.g., hypothesis testing, confidence intervals, generalizability, regression model assumptions, the coefficient of determination). Overall, for anyone interested in studying data science, the simple linear regression model is a great place to start!
Sources
“Lesson 1: Simple Linear Regression.” Penn State Eberly College of Science. https://online.stat.psu.edu/stat501/lesson/1.

Comments