Growing up, one of my favorite films was Studio Ghibli’s The Wind Rises—an animated historical drama about a 20th-century Japanese engineer named Jiro Horikoshi. Each time I rewatched it, I was always intrigued by a device that Jiro used for performing calculations. It consisted of two wooden rulers, with the top one able to slide freely. Somehow, in what seemed like magic, Jiro could slide the middle ruler and multiply any two numbers together, say 2.18 x 3.62, and by looking at the image below, obtain the correct answer of 7.89.
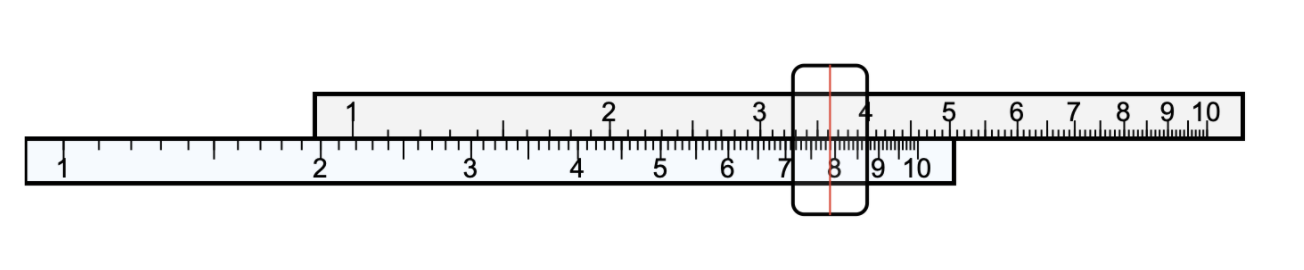
Except that it wasn’t magic; it was math.
The simple, clever math that makes a slide rule capable of multiplication is in fact the basis of an analog computer.
Exponentiation and Logarithms
Consider a number denoted by the letter b. When you multiply b by itself, n times, you are performing an operation called exponentiation. Specifically, we can write b × b × … × bn times = bn
We call b the ‘base’ and n the ‘exponent.’ For example, let the base be 10 and the exponent be 3. Since 1000 = 10 × 10 × 10 = 103, we say that 10 ‘raised to the power of 3’ is 1000.
A number that is multiplied by itself has the interesting property that
bn x bm = b × b ×… × bn times × b × b ×… × bm times = b × b × … × b n + m times = b n + m
An example of this is 101 x 102 = 10 × 100 = 1000 = 103. Notice, this property allows us to relate the multiplication of two terms with the addition of exponents. Hold on to this fact; it will be crucial shortly.
We are now ready to define a logarithm, which is the inverse function to exponentiation. A logarithm answers the question: ‘how many times must you multiply b by itself to obtain the number x?’ Equivalently, if we choose x and want to know the n for which x = bn, then the answer is n=(x) . If you plug in our solution for n in the expression for x, you should see that x = bx; the logarithm undoes the exponentiation.
Now the fun part: for our property bn x bm=bn+m, let n=(x) and m=(y) . With this replacement, we find that
b(x × y) = x × y = bx x by =b(x) +(y)
The base for the left and right sides is the same, so for them to be equal the exponents must be equal. We arrive at the expression that allows a slide rule to function:
(x × y) =(x) +(y) .
Notice, we have related multiplication again with addition.
Slide rule mathematics
Let’s examine the expression above carefully. If we could 1) calculate the logarithms of x and y, 2) add them, and 3) somehow undo the logarithm of the sum, we would find the value of x × y! A slide rule performs these three steps.
For the first step, notice that the digits of a slide rule are different from a typical ruler:

For instance, the separation between 1 and 2 is larger than the separation between 2 and 3. This is because the digits are arranged along a logarithmic scale. The full length of the slide ruler is logb10 - logb1 = logb(10/1) = logb10 , which for most slide rules is 10 inches. Exponentiating both sides yield 10 = b10, such that b = 1.26. As a result, the distance between 1 and 2 is 3.01 inches, while the distance between 2 and 3 is 1.76 inches.
The power of the logarithmic scale is that (x) and (y) are calculated for us.
If we pick a value x on the top ruler, say 3.62, and a value y on the bottom ruler, say 2.18,
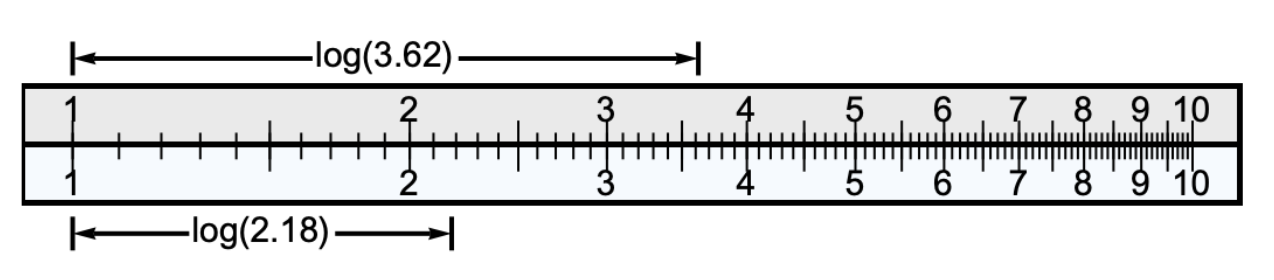
then their logarithm is simply the physical distance from the left side of the ruler.
For the second step, we simply push the top ruler by the distance (y) by aligning the left side of the top ruler with the position y of the bottom ruler:
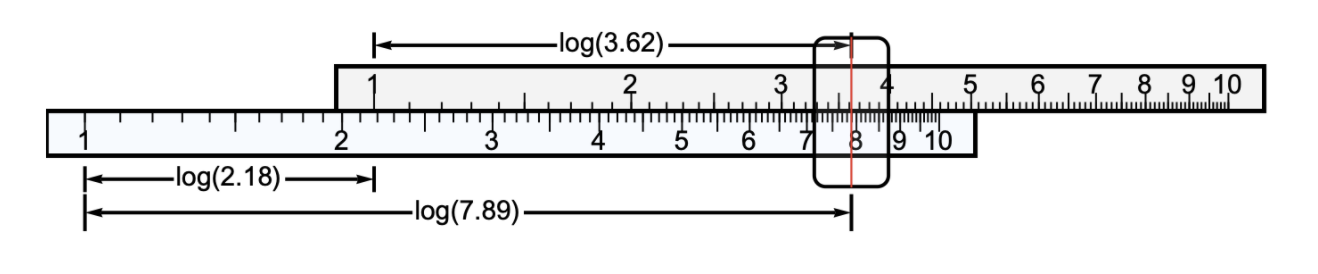
As is illustrated above, this push allows us to create the physical distance corresponding to (x) +(y) between the left side of the bottom ruler and the position of x on the top ruler.
Finally, we look at the value on the bottom ruler beneath x. This value is the product of x and y, since by converting between physical distance to the ruler, we undo the logarithm (x × y) and, at last, obtain x × y.
Slide rule considerations
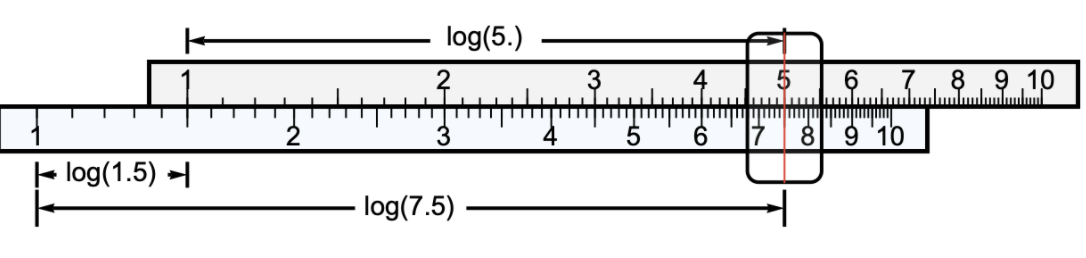
To strengthen your understanding, I provide a second use of the slide rule to compute 1.5 x 5 = 7.5:
Sometimes, though, the slide rule is too short to perform a calculation. Consider the multiplication of 4 and 5 to produce 20:

Is this calculation not possible with this instrument?
Fortunately, it is possible. Instead of the image above, we can position the right side of the top ruler on y = 4:

The answer is 2, which as usual is given below the x = 5. Try to think about this for a second. Why would repositioning the top ruler lead to an answer that is 10 times smaller than we expect? The answer is that we have shifted the top ruler by its full length, 10 . As a result, we subtracted 10 from 20 , giving logb20 - logb10 = logb(20/10) = 2 . This shows that it is possible to multiply any two numbers using a slide rule, if we keep track of missing factors of 10.
Analog computers
To recap, the slide rule simplifies calculations by replacing multiplication with addition. What I find incredible is that the slide rule is only one of many objects that use physical phenomena to simply math. These objects are called analog computers, of which the slide rule is one of the simplest examples.
I’ll leave you with an additional example of an analog computer. In my research I study atoms with lasers, and I frequently send light through lenses. It can be shown that lenses are analog computers capable of modifying the light that passes through them to perform a mathematical operation called a Fourier transform. But showing this, and understanding what a Fourier transform is, is a topic for another day.


Comments