Among the most important topics covered in any college-level microeconomics course is that of how to solve constrained optimization problems, which involve maximizing or minimizing the value of some objective function – such as a utility or cost function – subject to one or more constraints – such as a budget or production target. Although these problems can often seem quite abstract, the logic of constrained optimization has applications to an enormous array of real-world situations, including everyday decisions like how much of your income to spend versus save for the future.
The method of Lagrange multipliers is one approach to solving these types of problems.
In this two-part series of posts we will consider how to apply this method to a simple example, while highlighting some practical tips for how to remember the key steps.
As alluded to above, there are three basic elements of any constrained optimization problem:
- The objective function, which takes one or more arguments as inputs and returns a numerical value as an output;
- Whether the goal is to maximize or minimize the output of the objective function; and
- The constraint(s), or limits on which arguments can be validly considered when trying to find the optimal (maximum or minimum) value of the objective function.
A solution to one of these problems therefore consists of the argument(s) that, when plugged into the objective function, return(s) the maximum or minimum value that function can attain while also respecting the constraint(s).
To illustrate what this means in practice, let’s take a look at a concrete example.
Suppose that you are faced with the task of buying produce for the coming week, and that you have to decide how to allocate a budget of $18 among two items, avocados and bananas. (Unfortunately you don’t always have a terribly varied diet when you live inside of an economics problem!)
Your utility function, which describes how much satisfaction you get from a particular combination of avocados and bananas – sometimes called a “bundle” in economic parlance – is given by the expression:
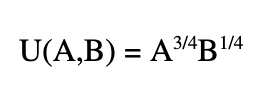
where A denotes the number of avocados and B the number of bananas purchased.
Suppose further that the price of one avocado is $1.50 and the price of one banana is $0.50. This means that your budget constraint can be written using the expression
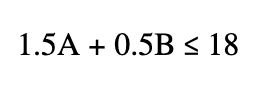
In other words, the total amount you spend on avocados (the price of an avocado times the quantity of avocados that you buy) plus the total amount you spend on bananas (the price of a banana times the number of bananas that you buy) has to be less than or equal to your budget of $18. (In some optimization problems the constraint will be an equality, but here we assume that it’s an inequality. In other words, you’re allowed to spend less than your full budget if it would make sense to do so.)
The objective function here is the utility function. Your goal is to maximize its value, since you want to get as much satisfaction as possible out of your haul of produce. The constraint is the budget you have available to spend, together with the fact that avocados and bananas are not free. The solution will therefore be the combination (or combinations) of avocados and bananas that maximizes your utility given what you can afford to spend.
The first step in applying the method of Lagrange multipliers is to set up the Lagrangian. This is a function that takes as its arguments the arguments of the objective function as well as another variable known as the Lagrange multiplier, which is usually denoted by the Greek letter λ (lambda).
In our example, the Lagrangian could be written in one of two different ways:
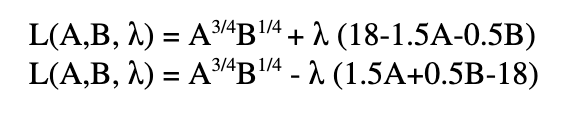
The underlying problem of choosing values for A and B in order to maximize the objective function is now converted into one of choosing values for A, B, and λ in order to maximize the Lagrangian.
This step can admittedly be a bit confusing. It might be tricky to remember how to set up the Lagrangian, how to know whether to add or subtract the term at the end, and/or what to put inside of the parentheses.
Here’s one way of thinking about it that may be helpful. Trying to maximize the Lagrangian effectively means trying to maximize the objective function while also getting extra credit for staying within your budget. If you have a total of $18 to spend, and $(1.5A + 0.5B) is the total amount that it costs to buy A avocados and B bananas, then $(18 – 1.5A – 0.5B) is the amount of money that you have left over. If what’s left over is greater than or equal to zero, you’ve stayed within your budget.
Congratulations! Staying within your budget is a good thing: it helps get you closer to your goal of maximizing the Lagrangian. This means that we want the term involving λ to make the whole Lagrangian expression larger. If we assume that \lambda is also greater than or equal to zero (more on this in Part Two), then if we put 18 - 1.5A - 0.5B inside the parentheses we want the term involving λ to be added into the Lagrangian.
Alternatively, we could think not in terms of extra credit for staying within your budget, but rather in terms of losing points for going over your budget. If we adopt this perspective, then the expression 1.5A + 0.5B - 18 tells us by how many dollars you went over your budget. Doing so is a bad thing from the perspective from maximizing the Lagrangian, so if we now put 1.5A + 0.5B - 18 inside the parentheses then we want the term involving λ to be subtracted from the Lagrangian.
In Part Two of this two-part series, we will consider the remaining steps to arriving at a solution to this example using the method of Lagrange multipliers, as well as how to verify that the solution we obtain is correct. Hope you’re hungry for some (imaginary) fresh produce!


Comments