
One day - in the not so far off future - when you’re an amazing lawyer (having first crushed the LSAT, of course), any witnesses you call to testify will have to swear to tell the truth, the whole truth, and nothing but the truth. Unfortunately, some truths are harder to determine than others. While we may be able to tell the truth about our own life experiences, things get a little trickier when it comes to the ‘truth’ of conditional statements.
In our first blog post on conditionals, we covered what conditional statements are, as well as going through the differences between necessary and sufficient conditions. The second post discussed manipulating conditional statements, so that you could find the inverse, converse, and contrapositive of a conditional (with a little help from Missy Elliott). In this post, we’ll be going over how a table setup can help you figure out the truth of conditional statements.
As a refresher, conditional statements are made up of two parts, a hypothesis (represented by p) and a conclusion (represented by q). In a truth table, we will lay out all possible combinations of truth values for our hypothesis and conclusion and use those to figure out the overall truth of the conditional statement.
Conditional statement truth table
It will take us four combination sets to lay out all possible truth values with our two variables of p and q, as shown in the table below. In the first set, both p and q are true. If both a hypothesis and a conclusion are true, it makes sense that the statement as a whole is also true. Take the conditional ‘If Claire buys a dog, I’ll help her take care of it’. If it’s true that Claire buys a dog and it’s true that I follow through on my promise to help her care for it (true hypothesis/true conclusion), then the conditional as a whole is true. However, if it’s true that Claire buys a dog but I decide to break my promise and not help her care for it (true hypothesis/false conclusion), then the conditional statement is proven false because the condition p that is supposed to imply the conclusion q did not actually do so.
It may seem to get trickier when you have a false hypothesis/true conclusion or false hypothesis/false conclusion, but there’s a rule that can help you out here: whenever the hypothesis or ‘p’ of a conditional is false, the conditional as a whole is always true. That’s because if the condition is never carried out, it doesn’t matter what the conclusion is - if Claire never gets a dog, I can never break my promise to help her take care of it. So, if your hypothesis is false, your conditional is always true. And the only way for your conditional to be false is if the hypothesis is true but its conclusion is false. Here you can look at a conditional truth table and compare it to another example statement given below:
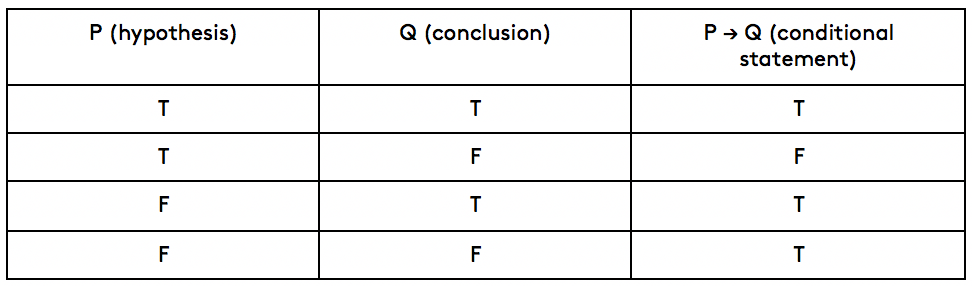
Let’s go through another example statement. Take the conditional ‘If Ivy does well on her test, she will pass the class’.
True p/true q: Ivy does well on her test, Ivy passes the class. The condition is met and the conclusion is met, so the conditional is true.
True p/false q: Ivy does well on her test, Ivy does not pass the class. The condition is met but the conclusion that is supposed to result from that condition does not occur, so the conditional is false.
False p/true q: Ivy doesn’t do well on her test, Ivy passes the class. You should know immediately that the conditional is true because the hypothesis or ‘p’ is false.
False p/false q: Ivy doesn’t do well on her test, Ivy does not pass the class. You should know immediately that the conditional is true because the hypothesis or ‘p’ is false.
Warning: Keep in mind that whether or not something seems true or is true in the real world doesn’t matter here. What matters is the logical outcome that you are able to find by using the truth table.
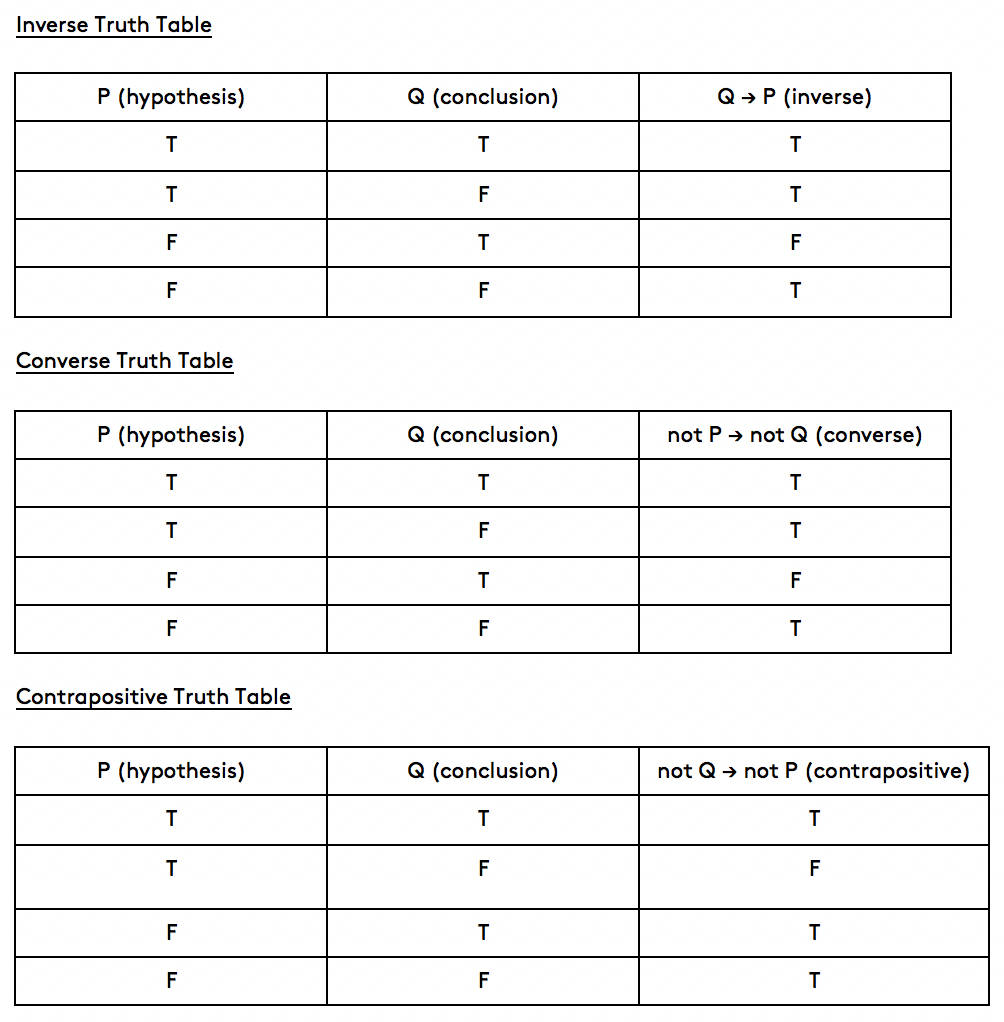
You can now put all three blog posts on conditionals into practice at once. Now that we’ve gone over truth tables for conditionals, try your hand at writing them out for the inverse, converse, and contrapositive. It may take a little bit to think through what the answers should be, but it will help you bring together all your knowledge on conditionals and their manipulations. The completed tables are below so you can check your work. Once you’ve written out these tables, attempt to work through them using real examples of conditional statements as we did above. The LSAT may not have much overlap with carpentry, but when it comes to building tables practice always makes perfect.
Comments