
In preparing for the quantitative section of the GMAT, students need to become proficient in a number of different math topics ranging from algebra to geometry. In addition to understanding how to approach these topics in a straightforward manner, students also benefit from developing an arsenal of strategies that can be applied to a variety of question types such as estimation, choosing smart numbers, and process of elimination. As the difficulty of problems increases, it becomes increasingly important for students to be able to move fluidly from one strategy to another, often combining more than one to solve a single problem. Let’s take a look at the following problem which is adapted from one I saw on the actual test:
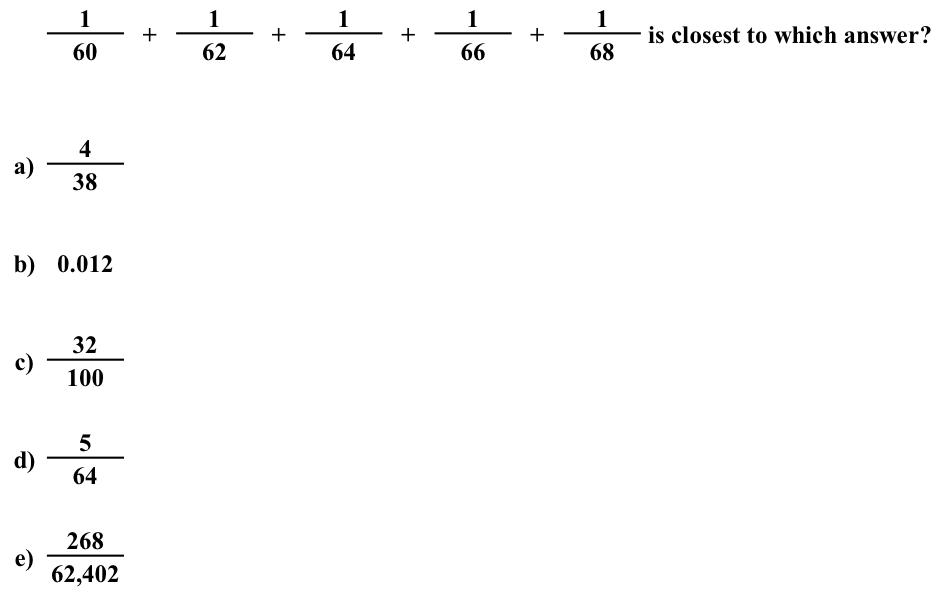
In order to navigate the quant section of the GMAT, students are taught (correctly) to look for certain markers of what type of problem they are faced with, and then proceed with a corresponding approach. In this instance, we see that the question involves adding fractions with different denominators, and as such the first approach that comes to mind is to find a common denominator.
By moving forward with this approach, however, we can quickly see that it will take an incredibly long amount of time and thus does not make sense to pursue. There are three different routes options available moving forward. The first and worst option is to keep trying to find a common denominator, perhaps by multiplying each denominator together. Doing this would be very time consuming as we previously noted. One of the biggest clues that you are falling in to a “trap” is that in order to execute a given approach, a ton of difficult calculations must be made.
The second approach is to either dump the question with a random guess or to use a quick form of estimation and process of elimination to make an educated guess. With a brief application of estimation, we can see that answers B and C are likely to be way off the mark (B, if written in fraction form would be close to 1 / 100, and C is close to 20 / 60).
The third and best approach is to take a step back, and try to find an alternate approach. Having the poise to do so is the key part of enacting “strategic flexibility”. We know the problem involves adding fractions, and we know that this is made difficult by the fact that we have dissimilar denominators that are not reduceable to common factors. What else do we notice? One thing that comes to mind is that the numerators are all the same number (1). Therefore if the denominators were the same, the numerator of the answer would be 5. Additionally, we can see that the denominators fall within a relatively close range of numbers, and that each one is 2 greater than the last. Thirdly, it is important to notice the question is asking us not for an exact answer, but for one that is closest to the actual number. This wording is usually a clue that some form of estimation, or inexact calculation is applicable. In this case, the easiest approach is to add up the numerators, and use the median denominator (64) as the denominator in the answer which gives you the fraction shown in choice D.
Using the median denominator makes sense as a method of estimating the actual denominator given what we know about fractions. 1 / 60 is a larger number than 1 / 68, so the average of the two numbers is likely something very close to 1 / 64. The key to arriving at this methodology is the willingness to think through the problem fluidly, and avoid getting fixated on one approach that may at first seem to be the best fit for the given type of problem.
Are you interested in connecting with a GMAT tutor like Ben?

Comments