The Intermediate Value Theorem explained by everyday life

Calculus can be tough stuff. Calc AB was the first AP class I ever took in high school, and though I love the subject now, I certainly didn’t love it when I was first struggling with limits or with the chain rule for derivatives.

Calculus is tough because it can seem so abstract. But the subject becomes a lot less scary when you look at real world examples that make the theories and equations more concrete and relatable.

Take the Intermediate Value Theorem (IVT), for example. In mathematical terms, the IVT is stated as follows:

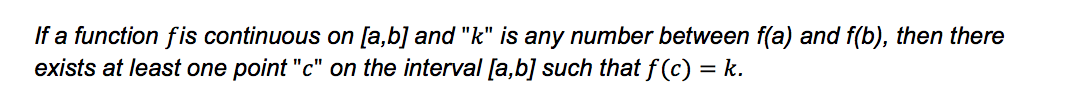
That definition might be confusing at first, especially if math isn’t your thing. But let’s try applying the IVT to real life - you might find that this theorem is something you already intuitively understand!

Example 1: Growth spurt.

In 7th grade, I was just over 5 feet tall (5’1”, to be exact). By the time I got to 11th grade, I was 6 feet tall.

So here’s the question: was there a time between 7th grade and 11th grade when I was 5’10” tall?

Let’s do another example that might be familiar to college kids...

Example 2: The “Freshman Fifteen.”

This is a hypothetical example. Purely hypothetical.

Suppose that on my first day of college I weighed 175 lbs, but that by the end of freshman year I weighed 190 lbs. According to the Intermediate Value Theorem, which of the following weights did I absolutely, positively, 100% without-a-doubt attain at some point during my freshman year?

A) 168 lbs

B) 178 lbs

C) 188 lbs

D) 198 lbs

The answer? B and C. If my weight on day one was 175 lbs and my weight at the end of the year was 190 lbs, I must have weighed every possible value between 175 and 190 at some point during the year.

If the logic behind that example makes sense to you, you’re well on your way to understanding one of the foundational theorems of calculus!

Conclusion

I hope these little anecdotes help demonstrate that the Intermediate Value Theorem isn’t an abstract idea you need to memorize in order to regurgitate it on a test. Rather, it can be presented in plain language, and you don’t need to be an expert in calculus to understand it.

Not every theorem you encounter in calculus can be explained in such a straightforward manner. But, if you have a teacher who is creative and knows their stuff, they can come up with examples that will help bring the abstract math down to earth 🙂.